Oftentimes, we want to estimate the memory usage for training a large model to avoid repetitive training launching which can incur significant computing cost. Therefore, I summarize the memory usage below such that one can estimate memory usage before start training. It's also a backbone estimation for other parallelism methods. $$ M_{total} = M_{m} + M_o + M_g + M_{a} $$ where $M_{m}$ is model memory usage, $M_o$ is optimizer memory usage, $M_g$ is gradients memory usage and $M_{a}$ is activations memory uage. I would also like to provide general notations below for computing memory usage throughout this blog. ### Notations #### Hardware * $d$: the number of GPU devices * $N$: the number of nodes #### Input * $s$: sequence length * $b$: batch size * $MB$: the number of micro-batch (for pipeline parallelism) - The corresponding micro-batch size is $\frac{b}{MB}$ (the number of data instances in a micro-batch). #### Model * $\theta$: the number of parameters for the full model * $L$: the number of transformer layers * $a$: the number of attention heads * $h$: hidden size * $k$: the number of bytes per parameter (for regular training). - $k_h$ the number of bytes per parameter in high precision (for mixed precision training). - $k_l$ the number of bytes per parameter in low precision (for mixed precision training). - $k=4$ for full-precision, $k=2$ for half-precision, $k=1$ for quarter-precision. #### Memory * $M$ total memory * $M_o$ Optimizer's Memory * $M_{a}$ Activations Memory, $M_{a}=M_{a1} + M_{a2}$ * $M_{a1}$ is activations within self-attention layers and MLP layers * $M_{a2}$ is activations within layer normalization layers and dropout layers. * $M_m$ Model's Memory ## Regular Training ### $M_m$ Model's Memory With regular training (no mixed precision), single model's memory takes $k \theta$. ### $M_o$ Optimizer's Memory The common Adam optimizer requires momentum $k \theta$ and variance $k \theta$, and it results in $2k \theta$ memory usage. 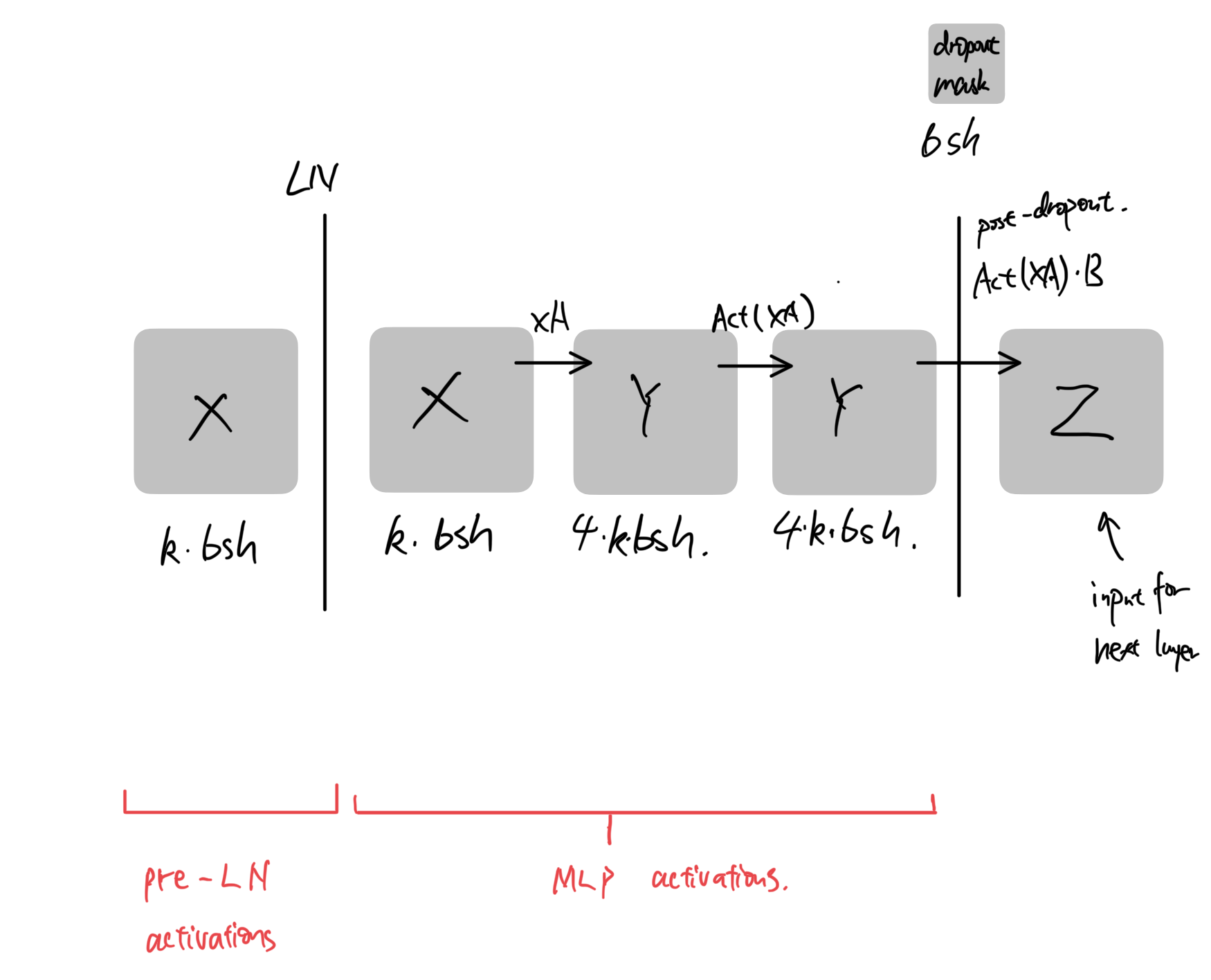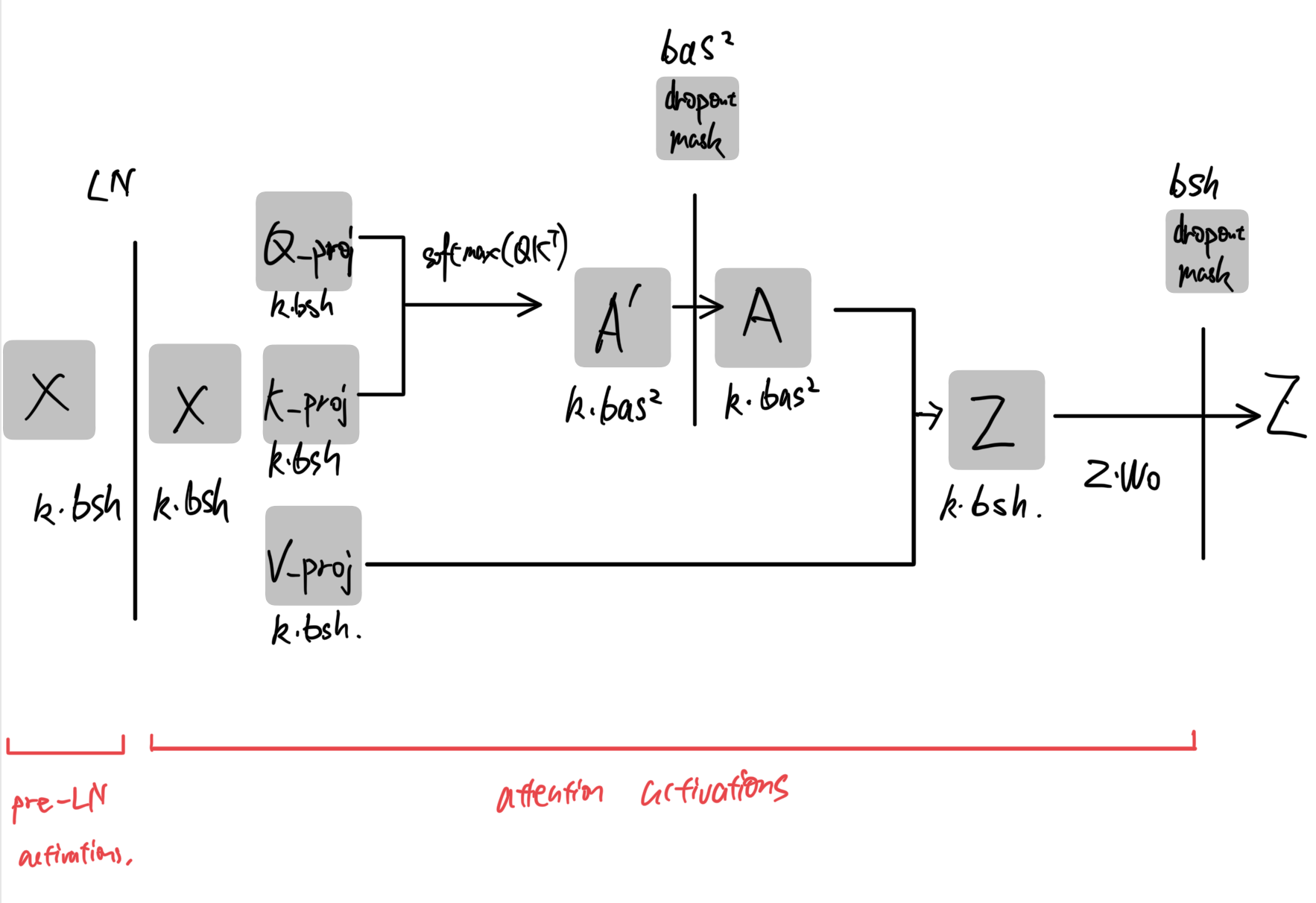### $M_g$ Gradients' Memory Consider that most parameters require gradients but some might not, we have conclude the following memory usage formula $$ M_g \le k\theta $$ ### $M_{a}$ Activations Memory #### MLP with LN  * pre-LN activations: $k \cdot bsh$ * MLP activations: $9kbsh$ * $M_{\text{MLP-activations}} = 10k\cdot bsh + bsh$ #### Self-Attention Layer with LN  * input, self-attention output(before projecting up) and QKV projections activations: $6k\cdot bsh$ * Attention logits: $2k\cdot bas^2$ * Dropout Mask: $bas^2 + bsh$ * $M_{\text{Attention-activations}}$ = $6k\cdot bsh + bsh + 2k\cdot bas^2 + bas^2$ * Note that this formula assumes MHA with Q,K,V projections $3k\cdot bsh$ as the graph suggests but GQA and MQA has less activations due to less key and value projections. I provide a more detailed formula below but it won't be used in this blog. $$M_{QKV} = k\cdot abs\frac{h}{a} + k \cdot \text{KVH}\times bs\frac{h}{a} + \text{KVH}\times bs\frac{h}{a} = k\cdot bsh + k \cdot \text{KVH}\times bs\frac{h}{a} + \text{KVH}\times bs\frac{h}{a} $$ where $KVH$ is the number of key/value heads and $\frac{h}{a}$ is head dimensions. 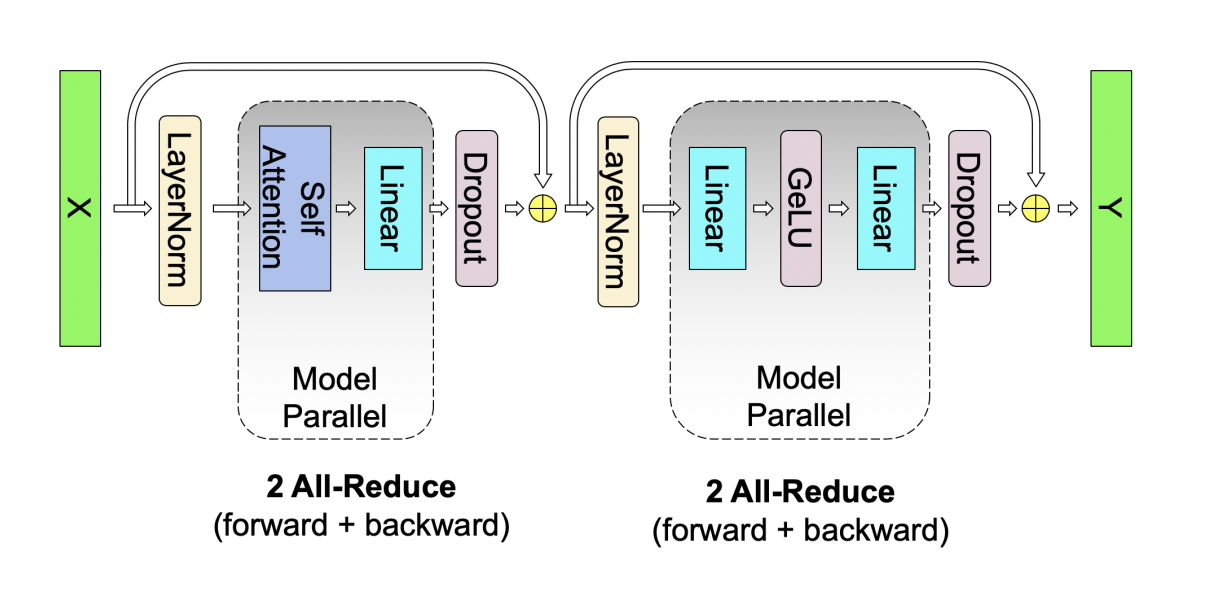#### Total activations  The graph above shows one transformer layer, and based on our previous calculations, we have $$M_\text{One-layer-activations} = M_{\text{MLP-activations}} +M_{\text{Attention-activations}}= 16k\cdot bsh + 2\cdot bsh + 2k\cdot bas^2 + bas^2$$. Considering the number of layers, we have total activations memory $$ M_a = L \cdot M_\text{One-layer-activations} = L(16k\cdot bsh + 2\cdot bsh + 2k\cdot bas^2 + bas^2) $$ ## Mixed Precision Training Classic mixed precision training is combining `fp32` and `fp16`, and nowadays it's engineered into even lower mixed precisions such as FP8 training in DeepSeek-V3. To make the formula to compute memory usage for different settings, I use $k_h$ and $k_l$ introduced in Notations section in the following formula. ### $M_m$ Model's Memory With mixed precision training, we have two model weights. One high precision model weight maintained by optimizer is computed into $M_o$. The other low precision model weight is for efficient forward operations, and it's computed into $M_m$. Therefore, the memory usage here is $k_l \theta$ ### $M_o$ Optimizer's Memory Now, Adam optimizer requires an additional high precision master model weight, and it results in $3k_h \theta$ memory usage. ### $M_g$ Gradients' Memory Considering gradients("learning") for each data batch is typically small, in mixed precision training, we often quantize it to lower precision. Therefore, we have $$ M_g \le k_l\theta $$ ### $M_{a}$ Activations Memory We can borrow the formula from Regular Training section, and activations memory are low precision as a consequence of low-precision model weights for forward pass. $$ M_a = L \cdot M_\text{One-layer-activations} = L(16k_l\cdot bsh + 2\cdot bsh + 2k_l\cdot bas^2 + bas^2) $$ ## Parallelism Techniques and corresponding per-GPU Memory Usage For training very large transformer models, not only we want to estimate the total memory usage, but also we want to ensure that its per-GPU memory usage is within the limit. I am sure all deep learning practitioners have seen `RuntimeError: CUDA out of memory` many times throughout his/her career, so this section is written to address per-GPU memory usage under different parallelism settings. As I have discussed memory partitioning in [DP blog](https://hepengfei.ml/blog/data_parallelism) and [HP blog](https://hepengfei.ml/blog/hybrid_parallelism), I will only briefly mention the incremental idea for each formula. Uppercase notations about parallelism such as $TP$ mean their parallelism size. For example, if tensor parallelism size is 8, then $TP=8$. Plus, as we are interested in per-GPU memory, $M_g$, $M_m$ and $M_a$ are all "local" tensors within one DP unit (one model replication) to simplify the computation. In this context, the following variables meaning change slightly * $b$ batch size / DP * $MB$ the number of micro-batch / DP ### Data Parallelism ##### DP/DPP $$M_o + M_g + M_m + M_a$$ * Under naive DP or DDP settings, each device maintains a full model replication(a.k.a model redundency) so there is no denominator in the formula. * $M_o$ could be omitted depending on whether the GPU maintains the optimizer. * I would like to stress again here that it's per-GPU memory usage, and only local activations within DP unit is counted towards $M_a$. The total memory usage across all GPUs should be $M_o + d(M_g + M_m + M_a)$ instead. ##### DP-Zero I $$\frac{M_o}{DP} + M_g + M_m + M_a$$ * Stage one shards the optimizer only. ##### DP-Zero II $$\frac{M_o+M_g}{DP} + M_m + M_a $$ * Stage two shards the optimizer and gradients. ##### DP-Zero III / FSDP $$\frac{M_o+M_g + M_m}{DP} + M_a $$ * Stage three shards the optimizer, gradients and the model. ### Tensor Parallelism $$\frac{M_o+M_g + M_m + M_{a1}}{TP} + M_{a2}$$ Here I divide $M_a$ into $M_{a1}$ and $M_{a2}$. * $M_{a1}$ is activations within self-attention layers and MLP layers which are **within the TP paritioning scope**. * $M_{a2}$ is activations within layer normalization layers and dropout layers which are **out of the TP paritioning scope**. * [Sequence parallelism](https://arxiv.org/pdf/2205.05198) is later introduced as TP + SP to optimize $M_{a2}$. Therefore, we have $$\frac{M_o+M_g + M_m + M_{a1}}{TP} + \frac{M_{a2}}{SP}$$ ### Pipeline Parallelism $$\frac{M_o+ M_g + M_m }{PP} + \frac{M_a}{PP \cdot MB}$$ * PP is not only one type of model parallelism but also divides activation into multiple stages(GPUs). - Its unique inter-layer parallelism enables it to partition every type of memory discussed here. * The actual activations' memory could be smaller considering at each given time it only process one micro-batch rather than a full batch. * $MB$ doesn't affect weight-related tensors, and it affects activations. ## Hybrid Parallelism ### TP + PP (a.k.a MP in my blog) $$\frac{M_o+M_g + M_m }{TP \times PP} + \frac{M_{a1}}{TP \times PP \cdot MB } + \frac{M_{a2}}{PP \cdot MB}$$ * Two MP methods paritions along different dimension, intra-layer and inter-layer. ### TP + PP + SP $$\frac{M_o+M_g + M_m}{TP \times PP} + \frac{M_{a1}}{TP \times PP \cdot MB } + \frac{M_{a2}}{PP \cdot MB \times SP}$$ * SP only optimizes $M_{a2}$ ### TP + PP + CP $$\frac{M_o+M_g + M_m }{TP \times PP} + \frac{M_{a1}}{TP \times PP \cdot MB \times CP} + \frac{M_{a2}}{PP \cdot MB \times CP}$$ * CP optimizes activations at all layers. ### DP-Zero1 + TP + PP + CP (popular 4D parallelism) $$\frac{M_o}{TP \times PP \times DP} + \frac{M_g + M_m }{TP \times PP} + \frac{M_{a1}}{TP \times PP \cdot MB \times CP} + \frac{M_{a2}}{PP \cdot MB \times CP}$$ * $M_o$ is additionally sharded by DP-Zero1. ### DP-Zero2 equivalent + TP + PP + CP (Llama3) $$\frac{M_o + M_g}{TP \times PP \times DP} + \frac{ M_m }{TP \times PP} + \frac{M_{a1}}{TP \times PP \cdot MB \times CP} + \frac{M_{a2}}{PP \cdot MB \times CP}$$ * FSDP in llama3 doesn't shard the model, and it's equivalent to DP-Zero2. * $M_g$ is additionally sharded by DP-Zero2. 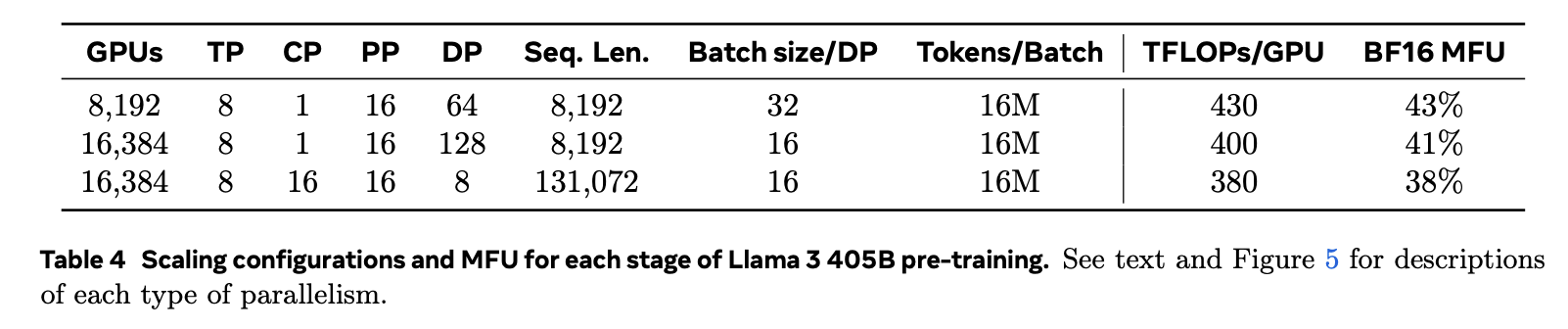## Examples ### Llama3  Let's compute the per-GPU memory for Llama3 long context pre-training(the third configuration) as it incoporates all parallelism sizes. #### Parameters From the graph above, we have * $s=131072$ for long context pre-training * $d=16384$ * $TP=8, CP=16, PP=16, DP=8$ - $N = TP\times CP \times PP \times DP = 16384$ - We can validate $d$ mentioned above as $d = N \times 8 = 131072$ (8xA100 per node) * $b=16$ batch size per DP unit. It only affects activation memory per model replication within one TP+PP group(one MP group). Other relevant configurations mentioned in the paper: * $k_l=2, k_h=4$ Mixed precision training with `bf16` and `fp32` * $L=126, d=h=16384, a = 128$ for 405B model. Note that they set the model dimension equal to the number of GPUs. * $PP = 16$, the number of micro-batch, $MB$, is denoted as $M$ in the original paper but I rename it to $MB$ for the purpose of differentiating it from memory variables. #### Memory Computation The computation is as follows: * all memory usage - $M_o = 405B \times 4 \text{ bytes/param.} \times 3 \times 10^{-9} \text{ GB/bytes}= 4860 GB$ - $M_g = 405B \times 4 \text{ bytes/param.} \times 10^{-9} \text{ GB/bytes} = 1620 GB$ full precision gradient accumulation. - $M_m = 405B \times 2 \text{ bytes/param.} \times 10^{-9} \text{ GB/bytes}= 810 GB$ `bf16` model for forward. - Within one DP unit, we have local activation computations $$ M_a = L(16k_l\cdot bsh + 2\cdot bsh + 2k_l\cdot bas^2 + bas^2) $$ $$= 126 (16* 2 * 16 * 131072 * 16384 + 2 * 16 * 131072 * 16384 + 2 * 2 * 16 * 128 * 131072^2 + 16 * 128 * 131072^2) $$ $$=147366233505792 \text{ bytes} \approx 147366 \text{ GB}$$. * Note that there is an overestimation here because the formula assumes MHA but llama3 uses GQA which hass less key, value activations than the computed volume. * We can summarize memory complexity for massive activation memory as $O(L(sh+as^2))$. In other words, it caused by large model dimension and long-context. That's also why PP (for $L$), TP (for high $h$) and CP (for high $s$) come into play. * with hybrid parallelism, we have the following approximated computation: $$ M \approx \frac{M_o + M_g}{TP \cdot PP \cdot DP} + \frac{ M_m }{TP \cdot PP} + \frac{M_{a}}{ TP \cdot PP \cdot MB \cdot CP} $$ $$ = \frac{4860 + 1620}{8 \cdot 16 \cdot 8} + \frac{ 810 }{8 \cdot 16} + \frac{147366}{8 \times 16 \times MB \times 16} $$ $$ \approx 6.3 + 6.3 + \frac{71}{MB} $$ The approximation slightly deviates from the true memory usage, and there are two reasons: 1. We first underestimate the per-GPU memory usage a bit by assuming TP also partitions $M_{a2}$. 2. We overestimate the activation memory by assuming MHA rather than GQA. Since we have 40GB memory per GPU, the final result gives ~27.4GB rest memory for activations. During training time, PP adjusts micro-batch size by $MB$. Based on the formula, as long as $MB \ge 3$, it fits into A100 GPU memory(40GB). However, so far, we haven't considered activation checkpointing yet. The original paper states activation checkpointing is not used for $s=8192$ pretraining, so I assume they enables it in long-context pretraining instead. Then we have an updated formula $$ \approx 6.3 + 6.3 + \frac{71}{MB\times AC} $$ where AC is the activation checkpointing factor meaning the ratio between activations saved for backpropgation and total activations. For example, if we only keep pre-LN activations for MLP with LN, $AC \approx 9$ which drives activations' memory down significantly. According to the paper, $MB$ is scheduled to be around $PP=16$ depending on batch size limit and the communication and computation efficiency. ## Q&A ### Q: Some training memory logical graphs show two model weights(in and out of optimizer) but some don't, why? * For regular training, only single model is needed. However, for mixed precision training, there are two model copies, one master weight and one "slave" weight. Master weight (usually full-precision) is managed by optimizer for parameter updates. Slave weights (usually half-precision) are quantized to lower precision for efficient forward operations. ### Q: Despite the computed memory is within limit, I still get OOM error. What should I do? 1. Try to reduce everything other than model size to see if it fits. Common settings are to minimize memory usages are - Switch to SGD optimizer rather than Adam optimizer. - $b=1, s=128$ and enable activation checkpointing to minimize activations. - Use DP-ZERO3 2. If it fits the memory, set back those settings one by one and launch training job. In this way, you can eliminate the possible causes. 3. If it doesn't fit, it's most likely the memory computation is wrong, and you need to double check.