Model parallelism in deep learning typically refers to partitioning the parameters (weights) of a model across multiple devices, such as GPUs, to reduce memory usage and accelerate training. One type of model parallelism is **tensor parallelism**, which partitions weight tensors along a specific dimension and keeps each partition on a separate device. This approach differs from **pipeline parallelism**, where different layers of the model are placed on different devices. In this blog, we will focus on **tensor parallelism**, assuming familiarity with communication operations such as `broadcast`, `reduce-scatter`, `all-gather`, and `all-reduce`. --- ## Weight Partition As illustrated in the figure below, we have a weight tensor with dimension $d_{in} \times d_{out}$. - **Row parallel**: Partition the weight tensor along the $d_{in}$ dimension. - **Column parallel**: Partition the weight tensor along the $d_{out}$ dimension. Each partition is stored on a distinct GPU and multiplied by its corresponding partition of the input during training.  Several questions might arise: 1. **What is the input tensor shape?** 2. **How does each GPU perform the $\text{matmul}$ operation?** 3. **How are input tensors and resulting tensors communicated and stored?** 4. **Can we combine the two parallel methods?** 5. **How are they applied in a Transformer architecture?** With those questions in mind, without further ado, let start with column parallel and row parallel. --- ## Column Parallel For the matrix multiplication $\mathbf{X} \times \mathbf{W}$ with dimensions $b \times d_{in}$ and $d_{in} \times d_{out}$, **column parallel** only requires $d_{out}$ to be divisible by the number of partitions (e.g., 2, 4, etc.). There is no restriction on the input tensor’s shape. ### Simplified Model Assume $\mathbf{X}$ has shape $1 \times 1$ and $d_{out} = 2$. Hence, $\mathbf{X} \times \mathbf{W} = \mathbf{Y}$ has dimensions $1 \times 2$. 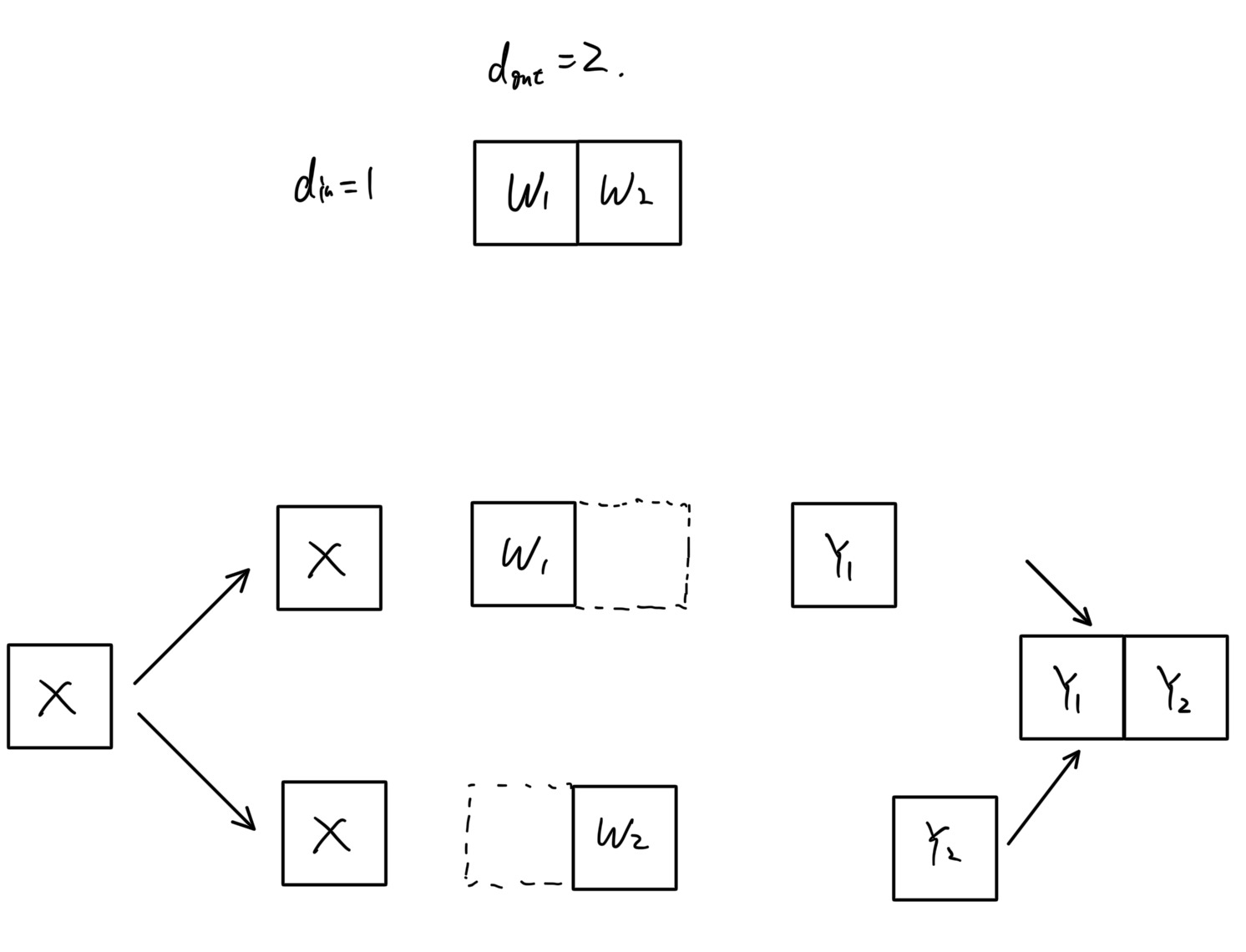In this setup:  1. **Broadcast** $\mathbf{X}$ to both GPUs so that each GPU can match the first dimension of $\mathbf{W}_1$ and $\mathbf{W}_2$. 2. **GPU 0** computes $\mathbf{X} \times \mathbf{W}_1 = \mathbf{Y}_1$. **GPU 1** computes $\mathbf{X} \times \mathbf{W}_2 = \mathbf{Y}_2$. Here, each partition $\mathbf{Y}_1$ and $\mathbf{Y}_2$ has shape $1 \times 1$. 3. Since the final output shape is $1 \times 2$, perform an **all-gather** of $\mathbf{Y}_1$ and $\mathbf{Y}_2$ to form the complete $\mathbf{Y}$. ### Full Model In a Transformer, $\mathbf{X}$ typically has shape $b \times s \times h$. The weight $\mathbf{W}$ has shape $h \times kh$. When using a tensor parallel size $TP$, we partition $\mathbf{W}$ across its second dimension into $TP$ chunks. Specifically: 1. **Broadcast** $\mathbf{X}$ to $TP$ GPUs to match the first dimension of each weight partition. 2. Each **GPU $i$** does the matrix multiplication $\mathbf{X} \times \mathbf{W}_i = \mathbf{Y}_i$. - $\mathbf{W}_i$ has dimension $h \times \frac{kh}{TP}$. - $\mathbf{Y}_i$ has dimension $b \times s \times \frac{kh}{TP}$. 3. **All-gather** the partial results $\mathbf{Y}_i$ across all GPUs to construct the full $\mathbf{Y}$ with shape $b \times s \times kh$. --- ## Row Parallel For $\mathbf{Y} \times \mathbf{W}$ of shape $(b \times d_{in}) \times (d_{in} \times d_{out})$, **row parallel** requires $d_{in}$ to be evenly partitionable. ### Simplified Model Assume $d_{in} = 2$ while keeping $b$ and $d_{out}$ at 1. Thus, $\mathbf{Y} \times \mathbf{W} = \mathbf{Z}$ has dimensions $1 \times 2 \times 2 \times 1 = 1 \times 1$. 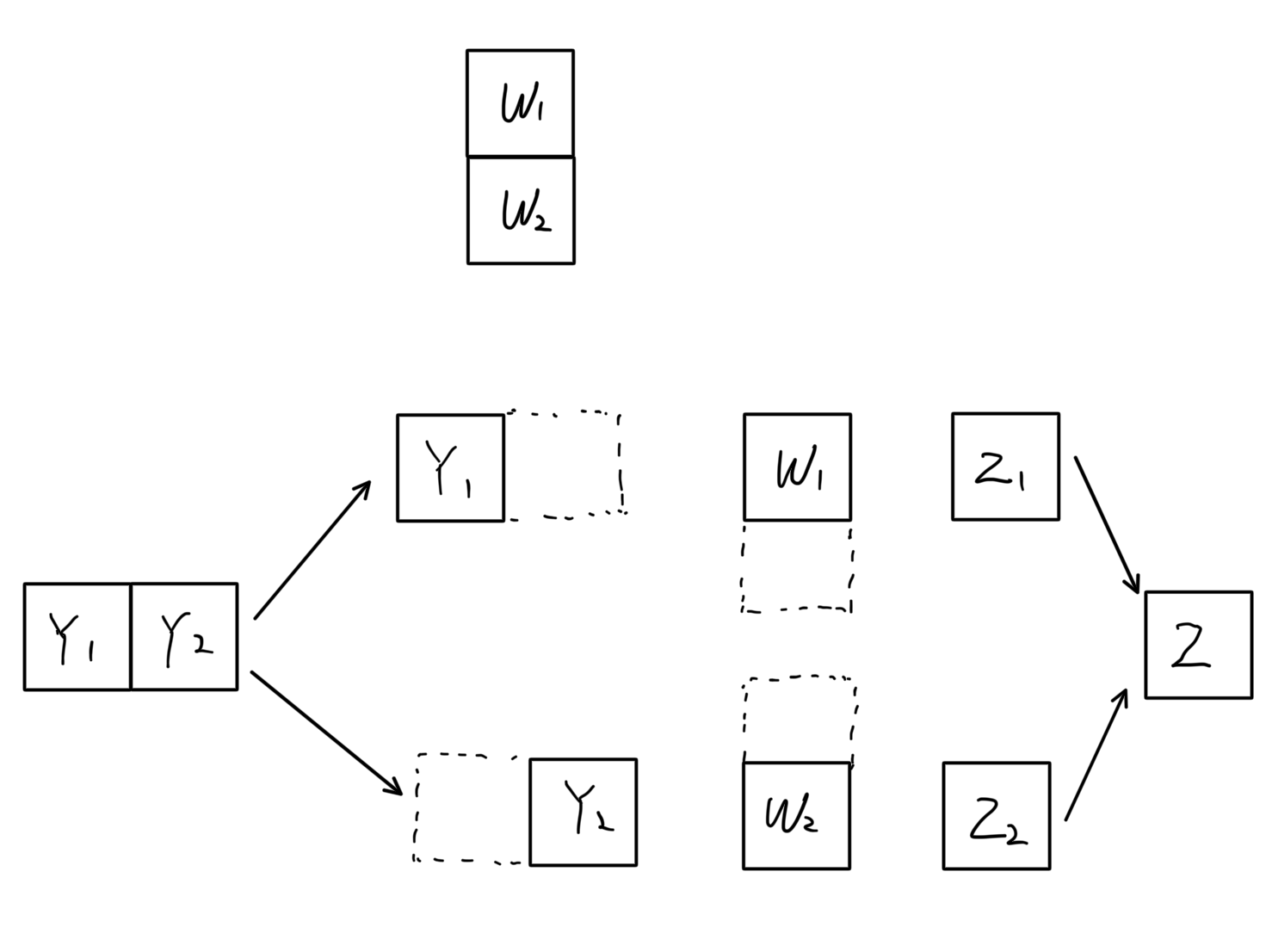The steps are:  1. **Scatter** $\mathbf{Y}$ across two GPUs, matching the first dimension of $\mathbf{W}_1$ and $\mathbf{W}_2$. 2. **GPU 0** computes $\mathbf{Y}_1 \times \mathbf{W}_1 = \mathbf{Z}_1$. **GPU 1** computes $\mathbf{Y}_2 \times \mathbf{W}_2 = \mathbf{Z}_2$. 3. Since the final result $\mathbf{Z}$ is $1 \times 1$, perform an **all-reduce** on $\mathbf{Z}_1$ and $\mathbf{Z}_2$ (often summation or averaging). ### Full Model In a typical Transformer setup, $\mathbf{Y}$ has shape $b \times s \times kh$, and $\mathbf{W}$ has shape $kh \times h$. With a tensor parallel size $TP$, we partition $\mathbf{W}$ across its first dimension: 1. **Scatter** $\mathbf{Y}$ such that each GPU gets $\mathbf{Y}_i$ of shape $b \times s \times \frac{kh}{TP}$. 2. Each **GPU $i$** computes $\mathbf{Y}_i \times \mathbf{W}_i = \mathbf{Z}_i$. - $\mathbf{W}_i$ has dimension $\frac{kh}{TP} \times h$. - $\mathbf{Y}_i$ has dimension $b \times s \times \frac{kh}{TP}$. 3. **All-reduce** the partial results $\mathbf{Z}_i$ to form $\mathbf{Z}$ with shape $b \times s \times h$. --- ## Column Parallel vs. 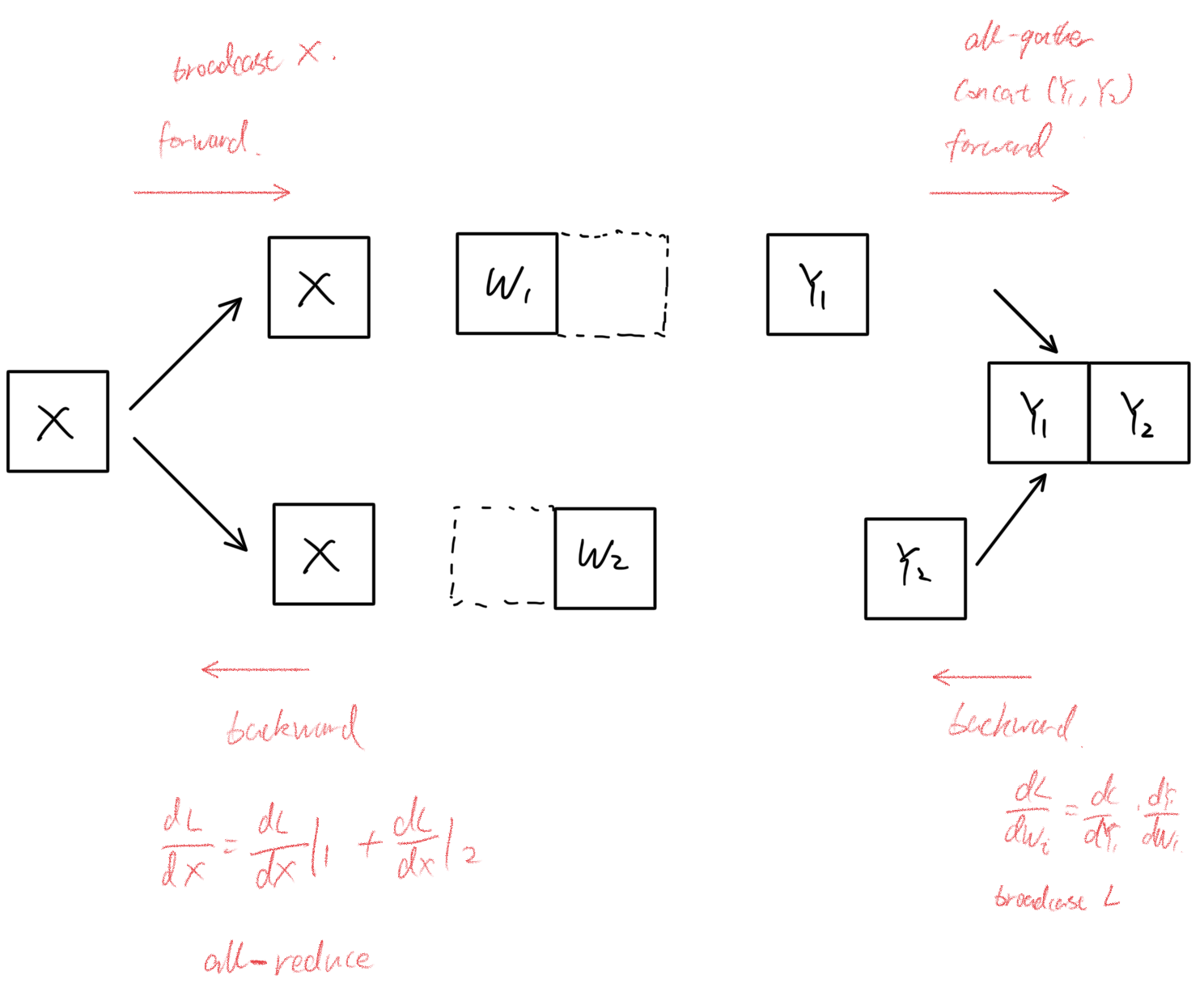Row Parallel Below is a comparison of the communication and matrix multiplication in both strategies: ### Column Parallel TP Communication  - In practice, we often replicate activations on all GPUs, so broadcasting $\mathbf{X}$ might be omitted if $\mathbf{X}$ is already present on all devices. - In the backward pass, each GPU only needs the loss (or gradients) broadcast to compute local gradients. 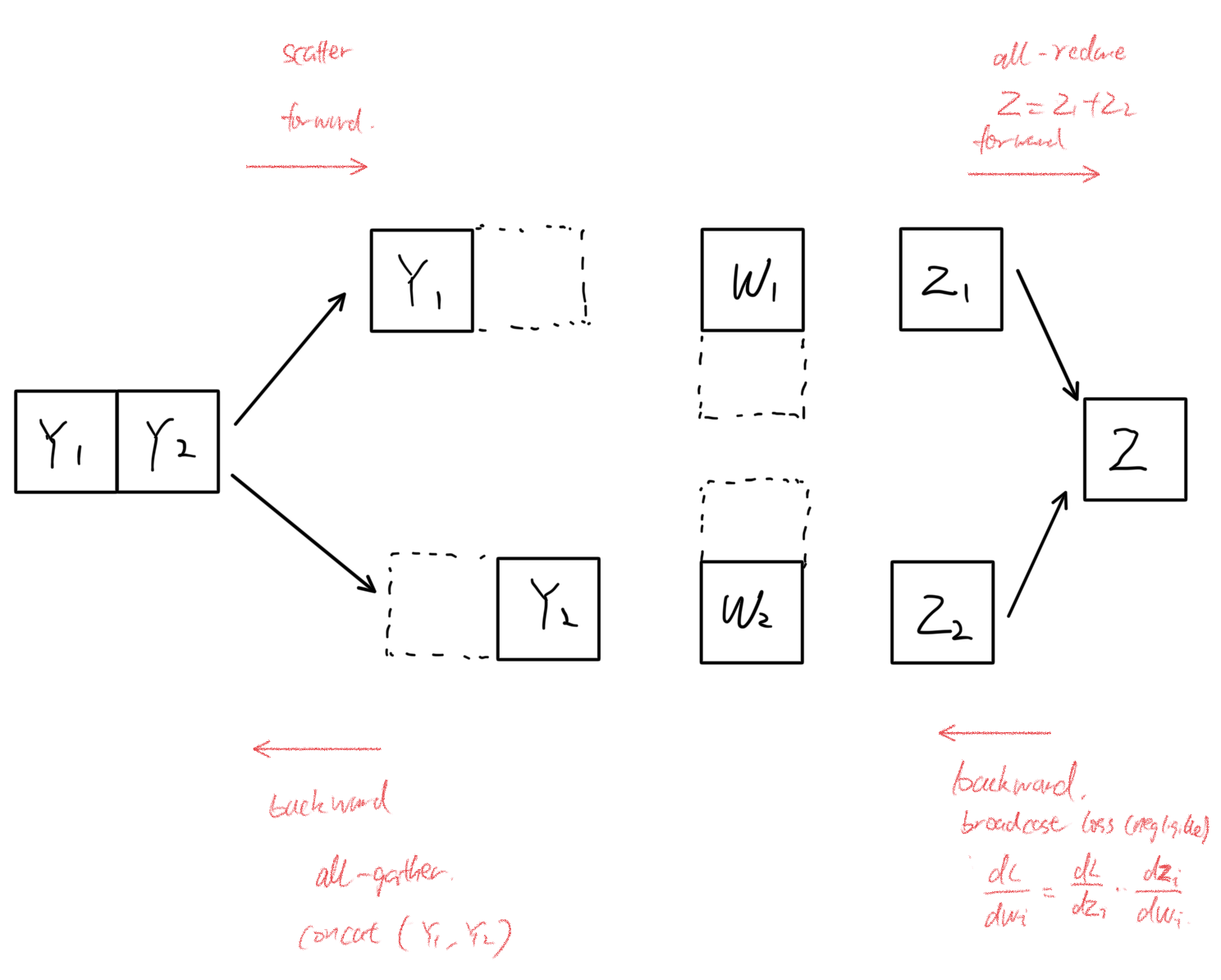### Row Parallel TP Communication  - **Broadcast $\mathbf{X}$** to multiple devices, then **all-gather** $\mathbf{Y}$. - Backward: $\frac{\partial}{\partial \mathbf{X}}$ is computed, then an **all-reduce** of gradients on $\mathbf{X}$. - **Scatter $\mathbf{Y}$** by the hidden dimension, then **all-reduce** $\mathbf{Z}$. 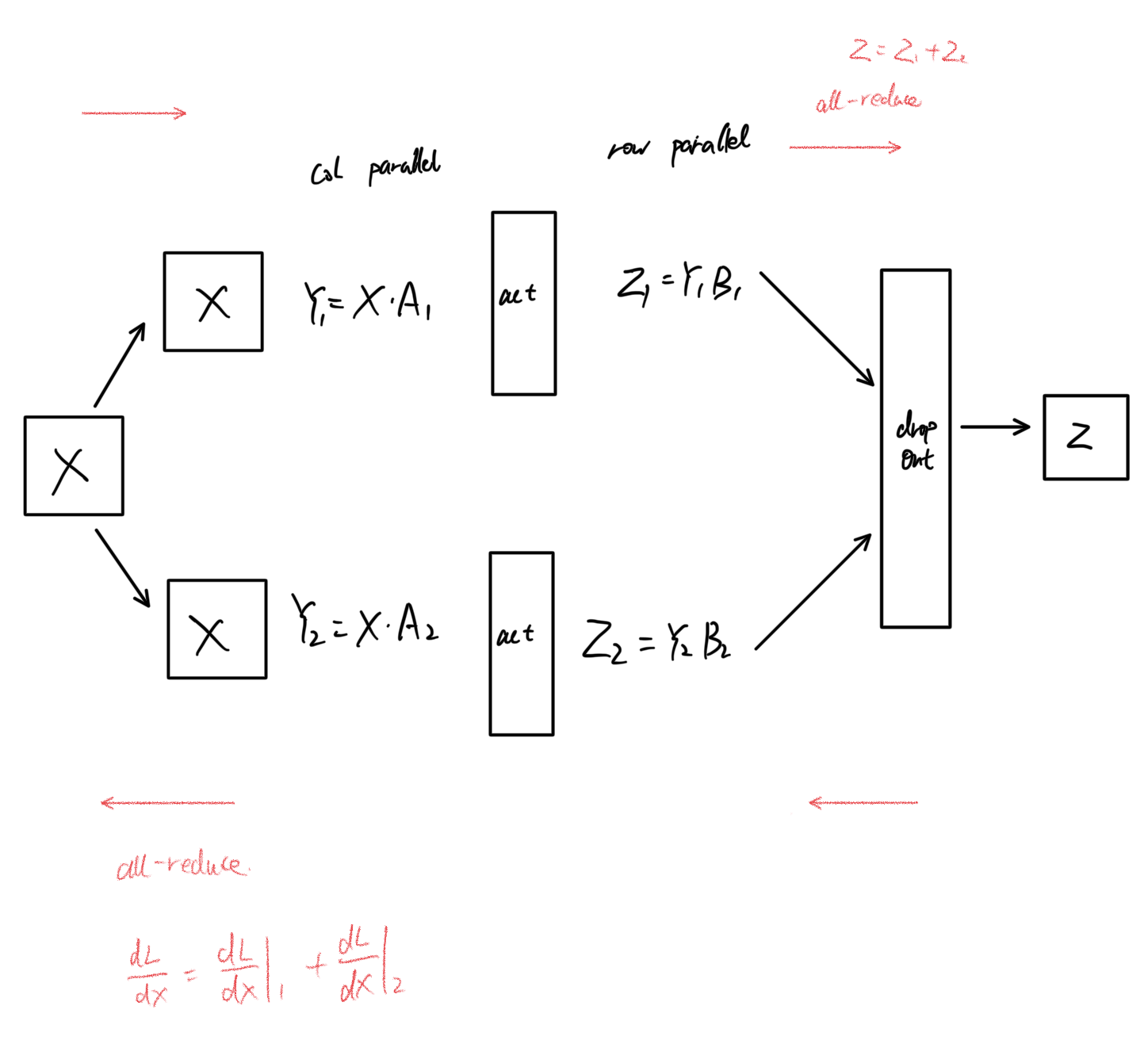--- ## Combining Column and Row Parallel Notice how the intermediate activation name changes from $\mathbf{X}$ to $\mathbf{Y}$ (column parallel) and then from $\mathbf{Y}$ to $\mathbf{Z}$ (row parallel). In practice, you can chain a column-parallel segment followed by a row-parallel segment so that intermediate activations on each GPU do not require communication. In other words, $\mathbf{Y}$ remains local to each GPU. Let’s see how this chaining appears in two common Transformer layers. ### MLP 1. $\mathbf{W}_1 : h \times 4h$ 2. Activation function (element-wise) 3. $\mathbf{W}_2 : 4h \times h$ Here, $k = 4$. Hence, $kh$ is $4h$.   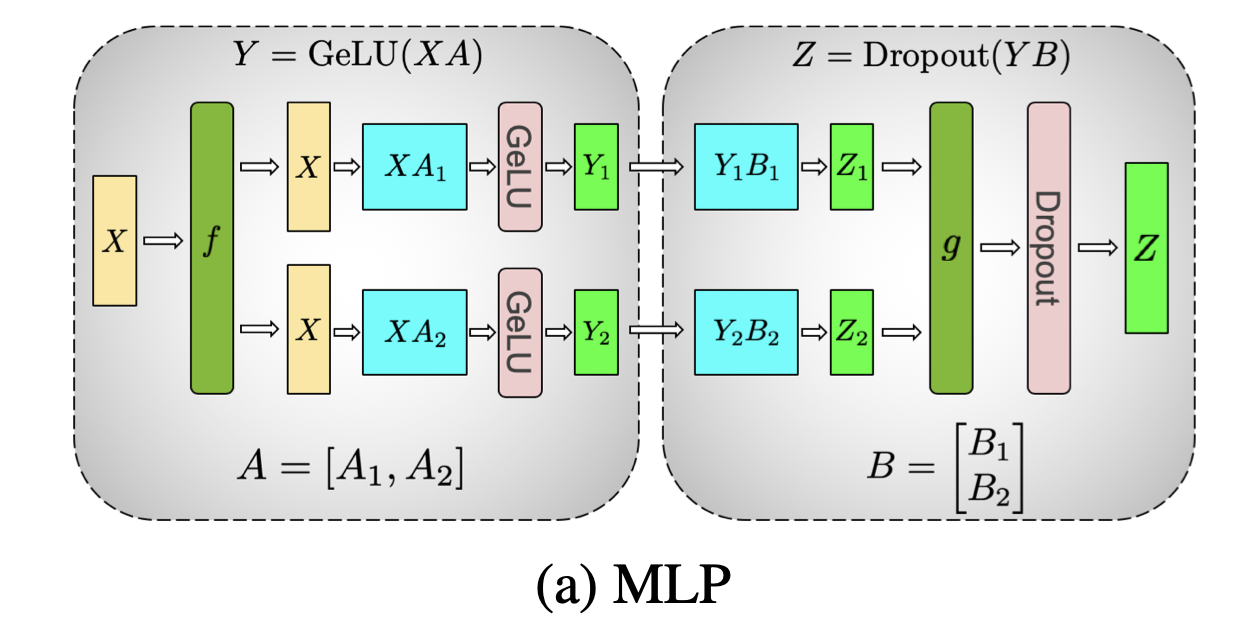In this communication flow, certain broadcasts are omitted: - We typically omit broadcasting $\mathbf{X}$ because each GPU already holds the full activation replication. - Similarly, after chaining column parallel, the communication between column-parallel output and row-parallel input can be avoided because each GPU’s local output can be consumed directly. The key communications are the **all-reduce** operations: - **Top-right all-reduce**: Summation of $\mathbf{Z}$ across devices. - **Bottom-left all-reduce**: Gradients $\frac{\partial L}{\partial \mathbf{X}}$ must be summed across GPUs because each GPU’s local $\mathbf{X}$ contributes partial computations with its local weight partitions. 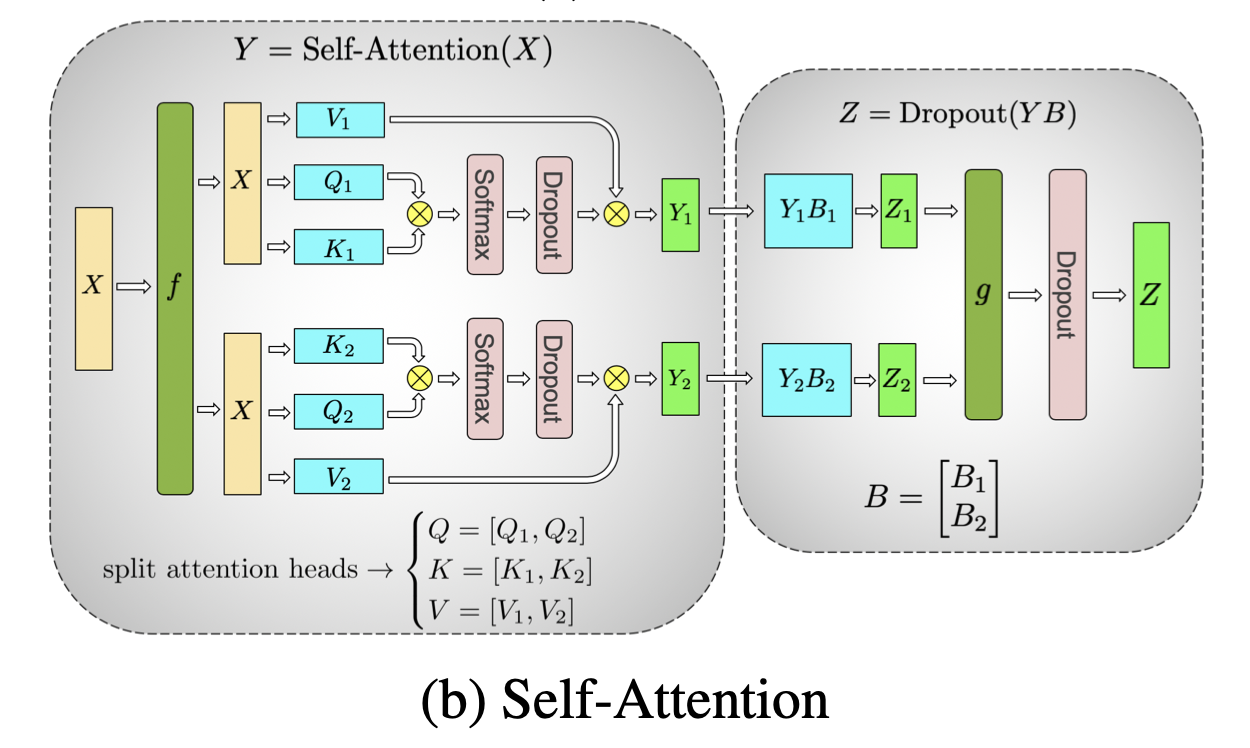### Self-Attention  - **Column parallel** partitions the weight tensors Q, K, V along the attention-head dimension $a$. - $\mathbf{X} @ [Q|K|V]$ yields $q_{\text{proj}} | k_{\text{proj}} | v_{\text{proj}}$. - Dimensions: $ (b \times s \times h) \times (h \times (h_{\text{head}} \times a)) \rightarrow b \times s \times h_{\text{head}} \times a $. - **Row parallel** uses a single linear projection from $h_{\text{head}}$ to $h$. - Let $B$ be $(h_{\text{head}} \times h)$, partitioned across the row dimension $h_{\text{head}}$. - Other than the noted difference, it shares the same parallel recipe and communication pattern as MLP layers. 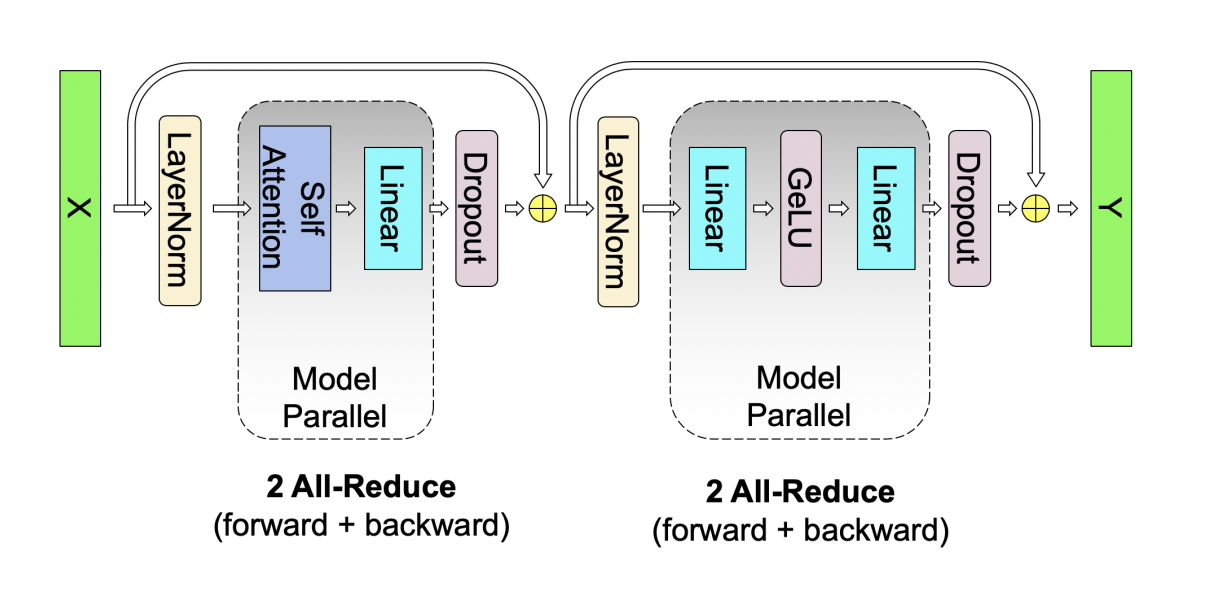--- ## Transformer Block Overview  Zooming out, a Transformer block is a repetition of an **MLP layer** and a **self-attention layer**. Each layer typically incurs one all-reduce in the forward pass and one in the backward pass. If the model has a total parameter count $\theta$, the communication volume for all forward and backward passes becomes $4\theta$ (two all-reduces per layer times two passes). --- ## What’s Next? So far, we have focused on partitioning weight tensors. However, intermediate activations within MLP and self-attention layers are also partitioned in column and row parallel approaches. Meanwhile, layers such as **Dropout** and **LayerNorm** often maintain a full copy of activations on each device, creating additional memory overhead. **Sequence parallelism** (SP) and **activation checkpointing** (CP) further reduce memory usage by partitioning activations and cleverly offloading them to CPU or recomputing them as needed. These are discussed in more detail in the [hybrid parallelism blog](https://hepengfei.ml/blog/hybrid_parallelism).