**Note:** This post continues our parallelism series and focuses on a technique called **Pipeline Parallelism** (PP). We will build upon the first blog (Data Parallelism) and gradually introduce more advanced pipeline concepts, culminating in a discussion about **DualPipe**—a new technique that helps reduce communication overhead in large-scale training. If you recall, the U.S. has banned certain high-bandwidth GPUs for export to China, but despite these constraints, a Chinese startup named DeekSeek developed **DeekSeek-V3**, a model comparable to GPT-4o while operating on relatively lower-bandwidth H800 GPUs. One key to their success is an innovative pipeline parallelism method, **DualPipe**. Let’s begin by revisiting layer parallelism. 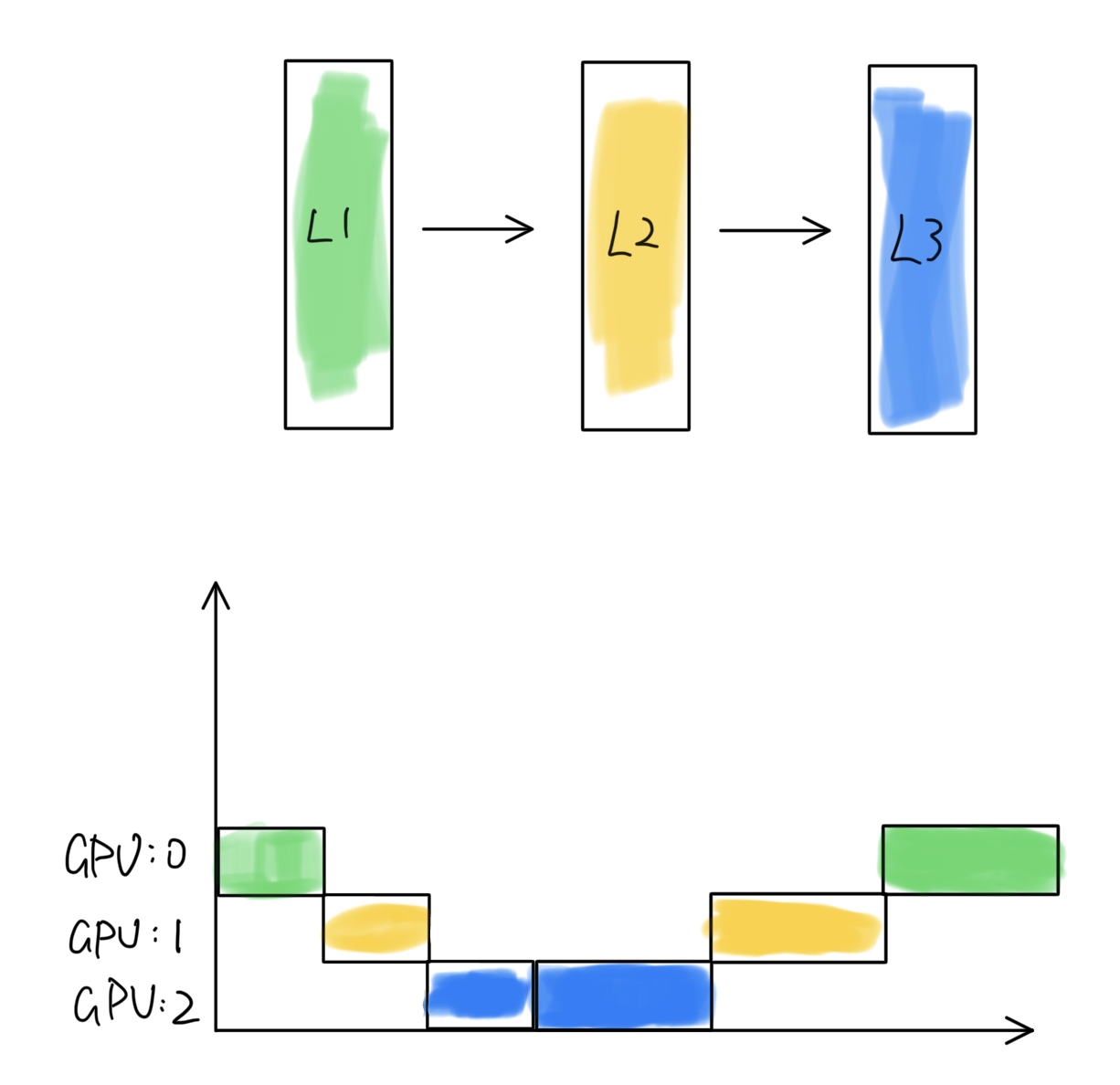--- ## Layer Parallelism (LP)  Consider a model with three layers and three GPUs. The top graph shows the logical view of the three model layers, and the bottom graph shows how they are mapped onto the three GPUs. Each layer occupies one GPU and processes one batch of data. - **X-axis**: Time - **Y-axis**: Pipeline stages (each stage corresponds to one GPU containing one layer) At the start, while `GPU:0` processes the first batch of data, the other two GPUs (`GPU:1` and `GPU:2`) remain idle. This idle time is referred to as a "bubble." ### Key Notations - $ M $: number of micro-batches (e.g., $ M = 1 $ in LP example and $ M = 3 $ in the next example) - $ N $: number of GPUs (also the number of pipeline stages), often referred to as $ PP $ in other literature - $ L_i $: the $ i $-th layer (or group of layers) - $ t_{fwd} $: forward pass time for one micro-batch - $ t_{bwd} $: backward pass time for one micro-batch ### Code Snippet (Basic Layer Placement) Below is a simplified code example that demonstrates how layers are placed on different GPUs during the forward pass: ```python class Model: def __init__(self): self.layer1 = SomeModuleClass() self.layer2 = SomeModuleClass() self.layer3 = SomeModuleClass() self.layer1.to(0) self.layer2.to(1) self.layer3.to(2) def forward(self, data): data = data.to(0) logits = self.layer1(data) logits = logits.to(1) logits = self.layer2(logits) logits = logits.to(2) logits = self.layer3(logits) return logits ``` Note that the backward pass is triggered by `loss.backward()` and proceeds in reverse order of the layers. ### Time Computation (Example with $ \text{mini-batch size} = 1 $) - **GPU idle time (bubble):** $6 t_{fwd} + 6 t_{bwd}$ - **Bubble rate:** $$ \frac{2t_{fwd} + 2t_{bwd}}{3t_{fwd} + 3t_{bwd}} = \frac{2}{3} $$ - **Total time:** $3 \times (t_{fwd} + t_{bwd})$ As we saw in the data-parallel blog, having a finer granularity can reduce bubble time. **Pipeline Parallelism** (PP) schedules forward and backward steps for each micro-batch in a staggered manner, reducing idle GPU time. 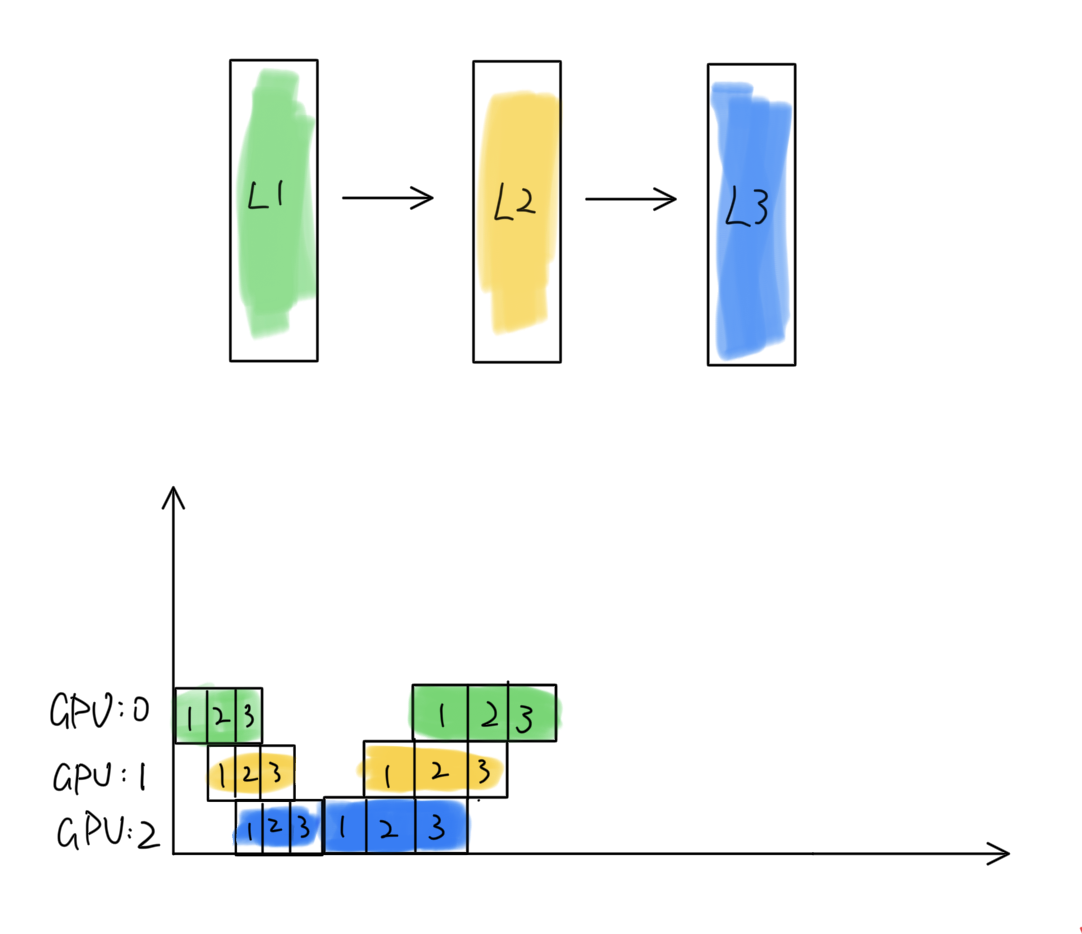--- ## Simple Pipeline Parallelism with $ M = 3 $  Visually, this pipeline parallel schedule shows fewer idle moments, leading to a shorter total processing time for one optimization step: $$ 5 t_{fwd} + 5 t_{bwd} $$ Let’s assume a mini-batch is split into $ M = 3 $ micro-batches, each with a single sample. For simplicity: 1. At $ t = 0 $, `GPU:0` begins processing micro-batch 1. The other two GPUs are idle at this time, creating $ 2t_{fwd} $ worth of bubble. 2. At $ t = 1 $, `GPU:1` receives activations for micro-batch 1 and begins its forward pass, while `GPU:0` starts micro-batch 2. Now the bubble is reduced to $ t_{fwd} $. 3. This pattern continues, overlapping some GPU operations and thus reducing idle times. ### Bubble Rate Formula $$ \text{bubble rate} = \frac{\text{bubble volume}}{\text{total GPU computation time}} = \frac{(t_{fwd} + t_{bwd}) \times (M-1) \times N}{(t_{fwd} + t_{bwd}) \times (M + N - 1) \times N} = \frac{N-1}{M+N-1} $$ Insights: - As $ M $ (the number of micro-batches) grows, the bubble rate shrinks. - **Layer parallelism** can be viewed as a special case of pipeline parallelism where $ M = 1 $. #### MP Definition Clarification - **Micro sense (Naive Model Parallelism / Layer Parallelism):** Each GPU holds one (or a group of consecutive) layer(s). The layer itself is not partitioned. - **Macro sense:** Involves combinations of data parallelism (DP) with various forms of model sharding, MP, TP and PP. In my blog about [hybrid parallelism](https://hepengfei.ml/blog/hybrid_parallelism), I refer MP as combining TP + PP for one model replication. --- ## Pipeline Parallelism Improvements  The figure shows a pipeline with $ M = 8 $ micro-batches, yielding a smaller bubble ratio than $ M = 3 $. However, simply increasing $ M $ is often limited by GPU memory constraints. Even then, a residual bubble ratio persists, which becomes more significant as the number of GPUs grows. Below are some key PP variants. ### 1F1B by [PipeDream](https://arxiv.org/pdf/1806.03377)  **1F1B** stands for “one forward, one backward.” Rather than waiting for **all** forward passes to complete before starting backward passes, **1F1B** triggers the backward pass of a micro-batch as soon as its forward pass finishes. - If $t_{bwd}=2t_{fwd}$, then the total time for **1F1B** is $3t_{fwd}$. - Because we interleave forward and backward passes of different micro-batches, the idle time (bubble) is reduced. ### Interleaved Scheduling by [LM-Megatron](https://arxiv.org/pdf/2104.04473)  Interleaving goes one step further by **splitting layers on each GPU** into multiple chunks, creating more granular and flexible forward/backward blocks. For instance, instead of assigning: ``` GPU 0: layers 1,2 GPU 1: layers 3,4 GPU 2: layers 5,6 GPU 3: layers 7,8 ``` We interleave them: ``` GPU 0: layers 1,5 GPU 1: layers 2,6 GPU 2: layers 3,7 GPU 3: layers 4,8 ``` This effectively creates two times more $M$ without increasing GPU memory usage, allowing finer-grained scheduling and reduced idle time. 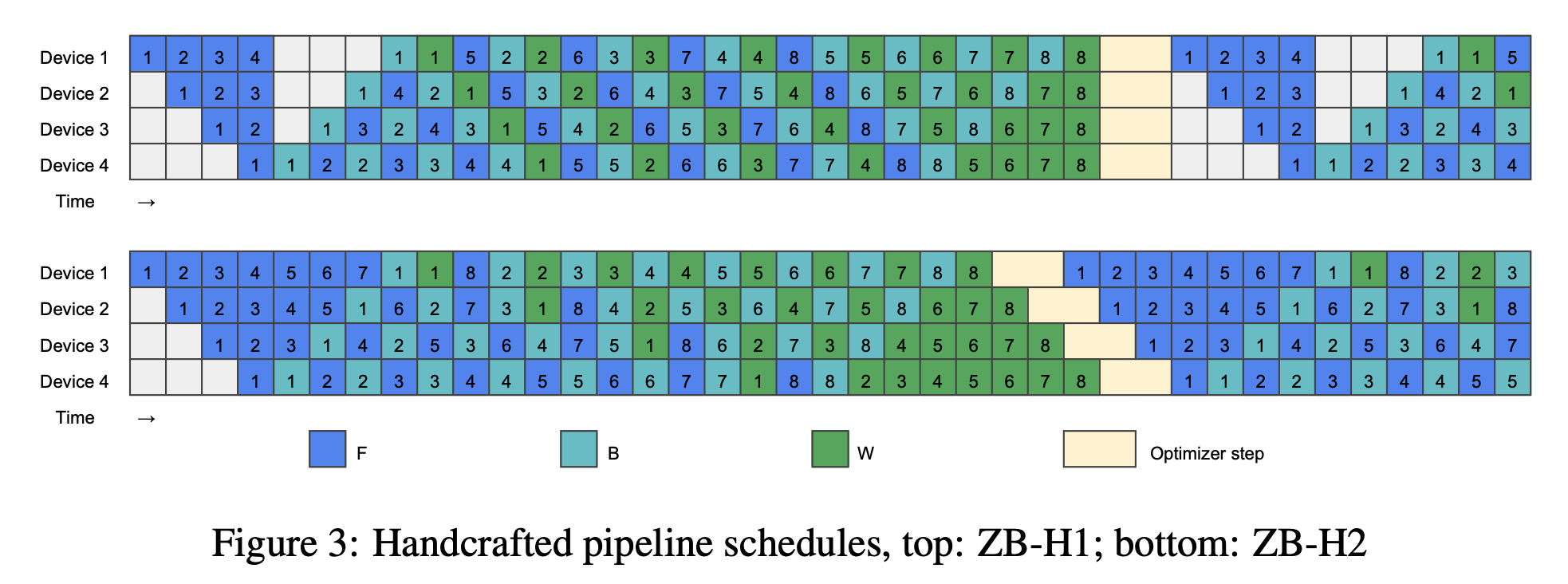### [ZB1P](https://openreview.net/pdf?id=tuzTN0eIO5)  ZB1P (Zero-Bubble 1 Pipeline) refines the backward pass by splitting it into smaller pieces so that **forward** and **backward** can overlap even more. Since backward needs to compute gradients w.r.t. both the **weights** and the **input activations**, ZB1P breaks these into sub-steps ($ t_b $ and $ t_w $). On the one hand, it matches $ t_{fwd} $. On the other hand, those operations can be completed at different times which allows more flexible scheudling. ### DualPipe by [DeekSeek-V3](https://arxiv.org/pdf/2412.19437)  DualPipe combines all the above principles: - It maintains **two model copies** within one PP group. - It splits the micro-batches into **two groups**. - It interleaves forward and backward passes (1F1B + ZB1P concepts), scheduling them to maximize overlap and minimize idle times. This approach drastically cuts down communication volume, which is particularly vital in **bandwidth-limited clusters** (such as China’s H800). The result? DeekSeek-V3’s training efficiency approaches that of models trained with high-bandwidth GPUs, even though they are using slower interconnects. --- ## Summarization Key takeaways for **Pipeline Parallelism**: 1. **Dynamic Task Scheduling**: Rearrange non-dependent computations (e.g., **1F1B**) to reduce bubbles. 2. **Problem Decomposition**: Breakding down computation and communication operations into finer granularity (micro-batch). - Smaller micro-batches and split backward passes yield more opportunities for parallelism. - Each operation’s memory footprint is smaller and lives for a shorter duration on the GPU, reducing both memory usage and communication overhead. - Backward is broken down into graidents w.r.t input activations and graidents w.r.t weights. 3. **asynchronous processing**: Overlap forward/backward passes and computation/communication wherever possible. As we see with **DualPipe**, engineering breakthroughs often stem from carefully overlapping tasks and splitting them into manageable chunks—especially under bandwidth or political constraints.