As a veteran NLP engineer with hands on experiences in various parallelism techniques, I find that the current offical framework documents/the original papers/random Medium blogs are often either nonintuitive, full of less relevant details or less illustrations which is hard for beginners to grasp the core ideas of them. Therefore, I plan to write a series of blogs with intuitive understanding on core ideas of several important parallelism techniques including data parallelism, tensor parallelism, pipeline parallelism, sequence/context parallelism and expert parallelism. All of these blogs will be written chronically with reasoning for each improvement. # Data Parallelism Evolution ## Data Parallelism Data Parallel (DP) is the foundational and most intuitive form of parallelism in model training. It partitions input data across batch dimension and replicates the model across multiple workers, and each worker processes a subset of the data batch. * Parameter Server(PS) Architecture: In the past, DP achieves multiple workers computing and synchronizing gradients by parameter server. It is originally proposed in multi-node training setting, but I resemble modern DP on multi-GPU to multi-node setting here. In practice, if you train model with DP on two gpus, you can observe they occupy uneven amount of memories. The reason is that one of two GPUs (typically the first GPU) acts like a parameter server stores and updates optimizer states. See the graph below. * During gradient communication, each worker (on one thread) is responsible for `push` and `pull` gradients at the same time to/from PS as shown on the right graph. Workers(single process multiple threads) contribute to the process actively.  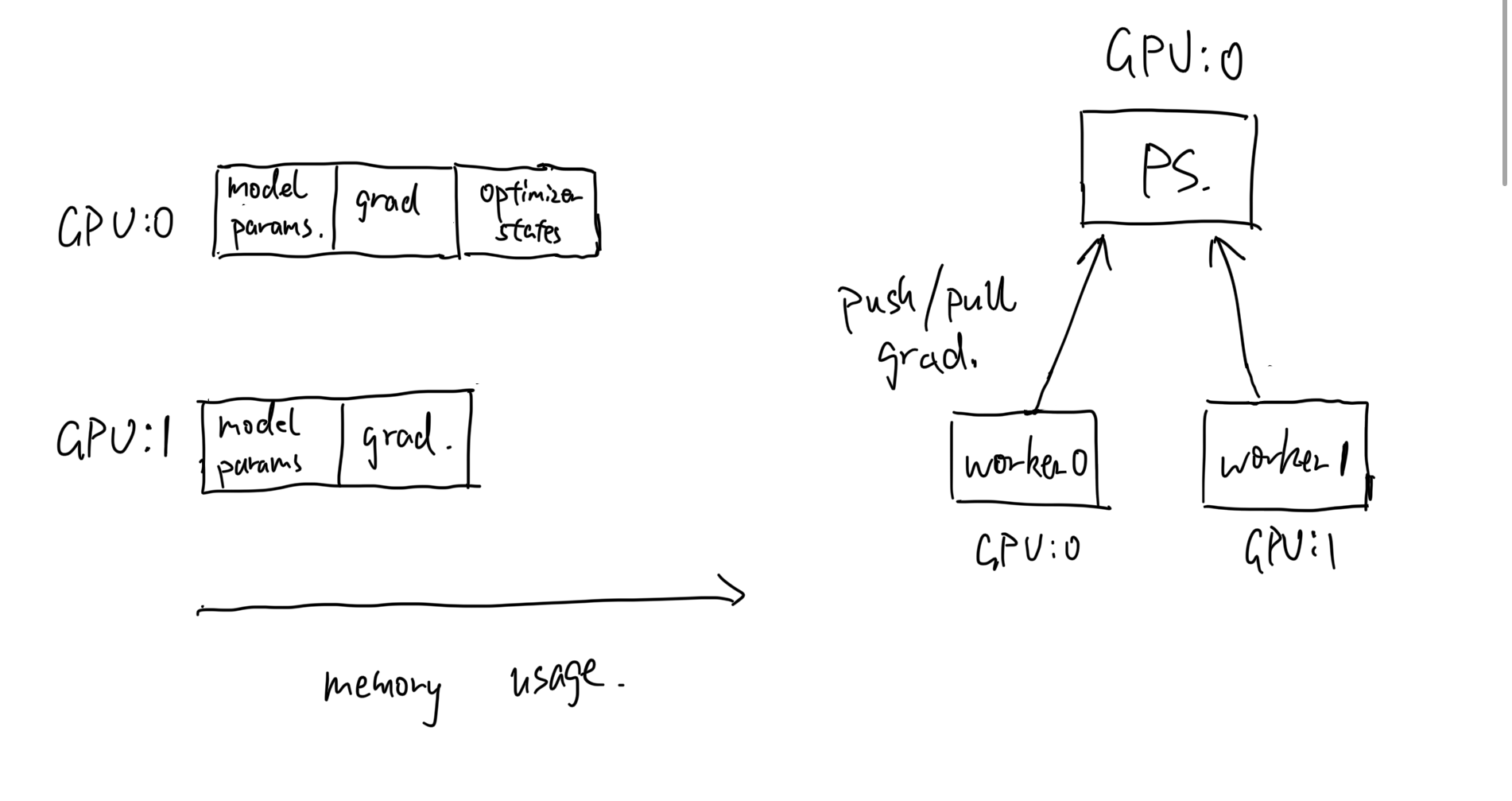However, as the number of workers grow, the communication volume upon pushing and pulling gradients incurs a sudden **communication overhead** which becomes a bottleneck for training speed. It's because all workers share the same bandwidth to one parameter server. ## Distributed Data Parallelism Distributed Data Parallel (DDP) enhances DP by launching multiple processes, where each process handles a mini-batch of data but maintain optimizer states independently. This approach speeds up training mainly by reducing peak communication overhead through efficient all-reduce communication operation. * No PS. In other words, all workers (multiple processes) on all GPUs participate gradients communication actively with its two "neighbour" GPUs. * During all-reduce communication, each GPU requires `send` and `rev` operation in a streaming ring-like manner, and this is enabled by multi-process.  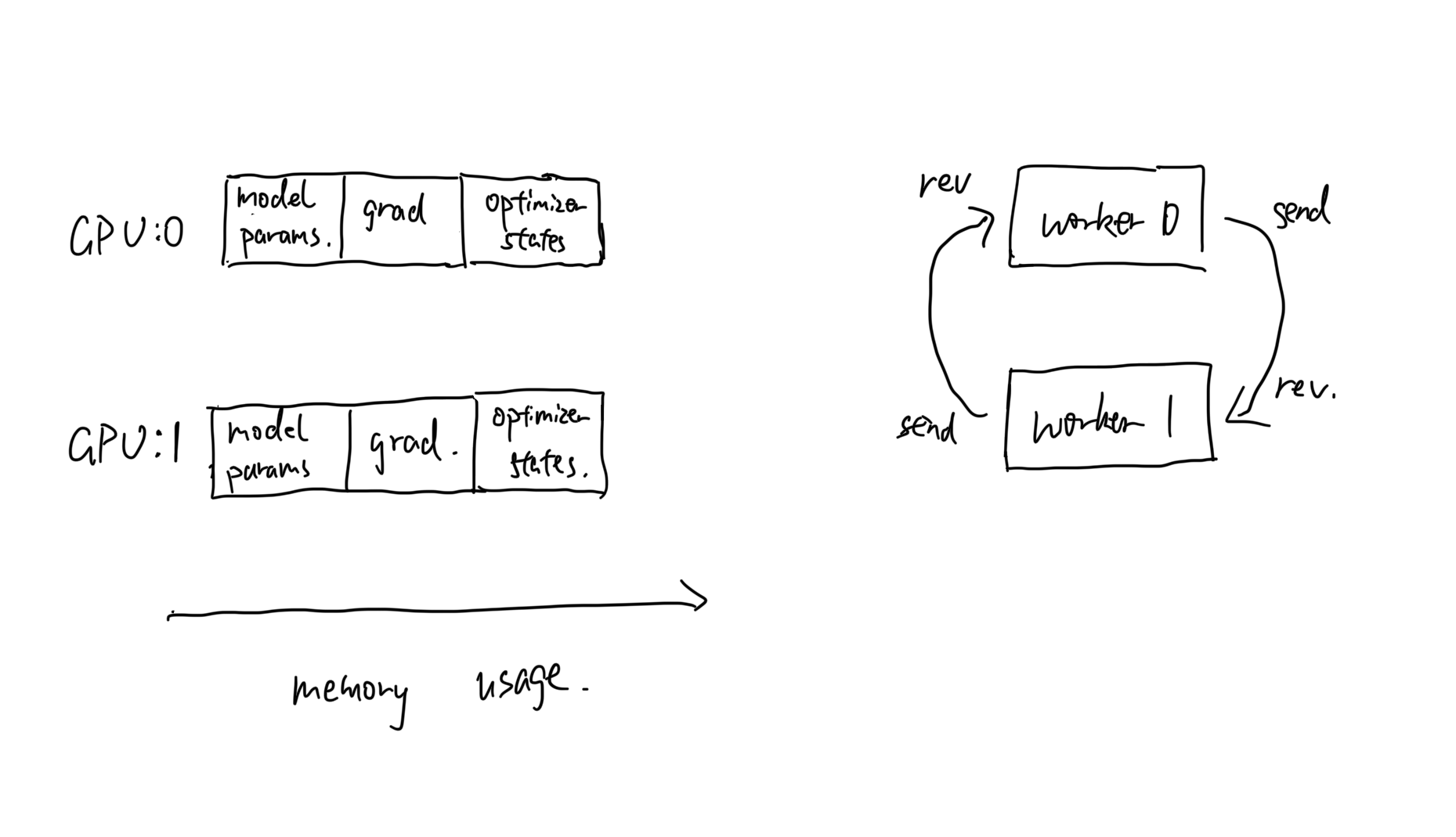Despite the communication improvement from DP to DDP, model and optimizer states remains replicated across GPUs. On the one hand, it enables simple and efficient optimization. On the other hand, such a replication lead to a lot of **redundant memory usage**. Can we optimize the redundancy? Deepspeed DP-Zero is proposed to solve such a problem. ## DeepSpeed DP-Zero Deepspeed DP-Zero has three stages, and it optimizes the redundancy incrementally in the three stages. Before we dive into stages, I would like to explain general notations in the graph. Dotted lines means these tensors don't persist during training time, and they are materialized upon computation needs and discarded after computation. Solid lines means the tensor persist on GPU memory during training no matter whether it's being used for computation. Upper case letter means full (model-wise) size tensors, and lower case with index means partial size tensors. Letters with hat means tensors are reduced(averaged) across GPUs. 1. **Optimizer States(O)**: During DP forward pass, optimizer states are not needed because there is no gradient update. Can we partition the optimizer states during forward pass and gather it during backward? Zero-1 handles this situation exactly -- with each GPUs hosts partial optimizer states, after all-reduce gradients $G$, it all-gather optimizer states to sync weights. 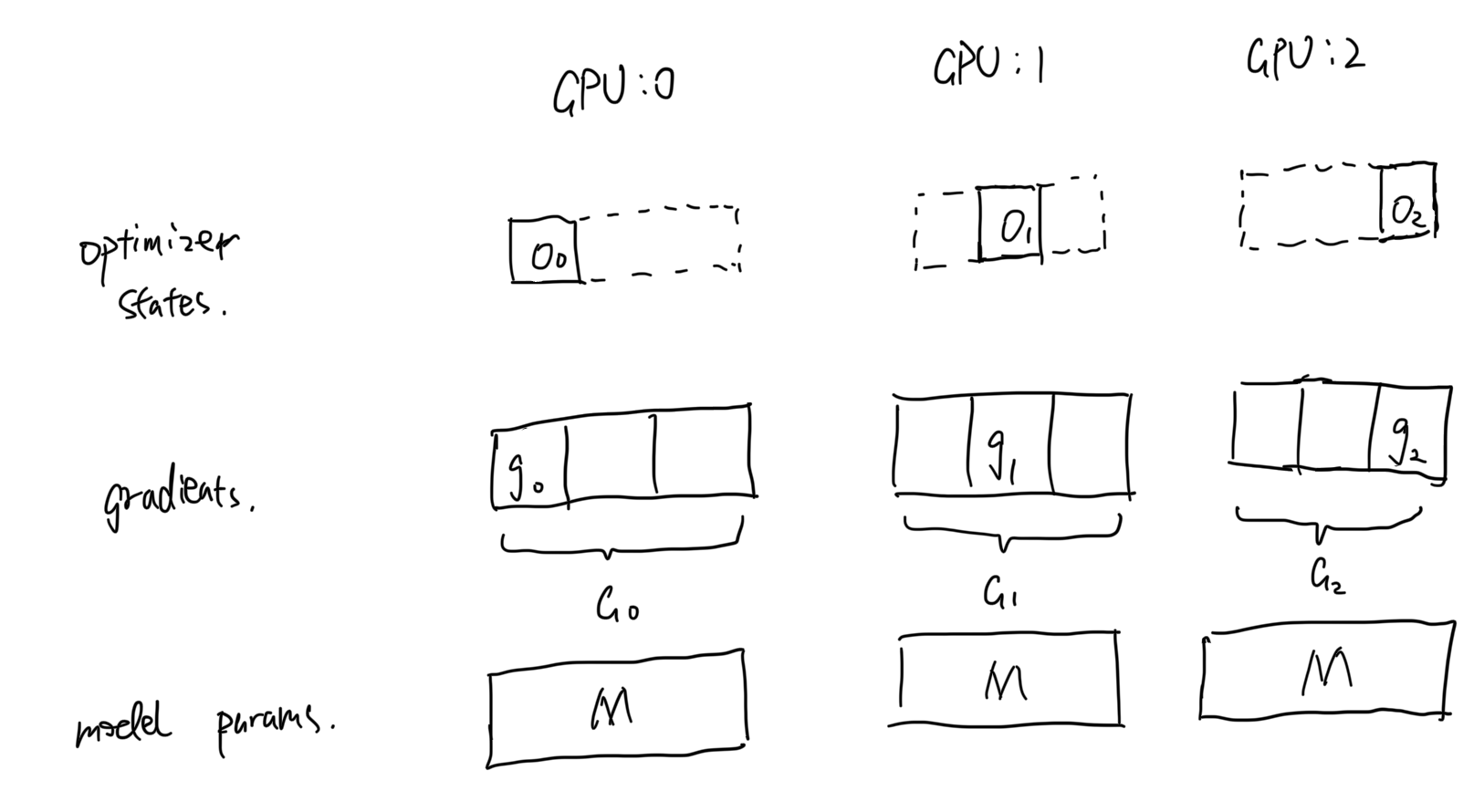 2. O + **Gradients(G)**: In Zero-1, averaged gradients after `all-reduce` $\hat{G}$ is equal to $avg(G_0, G_1, G_2)$. If you think deeply, each partial optimizer states only requires partial average gradients. For example, optimizer states $O_0$ only requires $\hat{g_0}$ to make an update but we gathered a full $\hat{G}$ in `gpu:0`. In Zero-1, we communicate the full gradients which is unnecessary for updating optimizer states. Therefore, in Zero-2, we should also partition gradients across GPUs and only gather gradients $\hat{g_i}$ that correspond to its partial optimizer state $O_i$.(The communication operation is actually called `reduce-scatter`) Therefore, it not only optimizes memory usage (on gradients) but also reduces communication from $3\theta$ to $2\theta$. 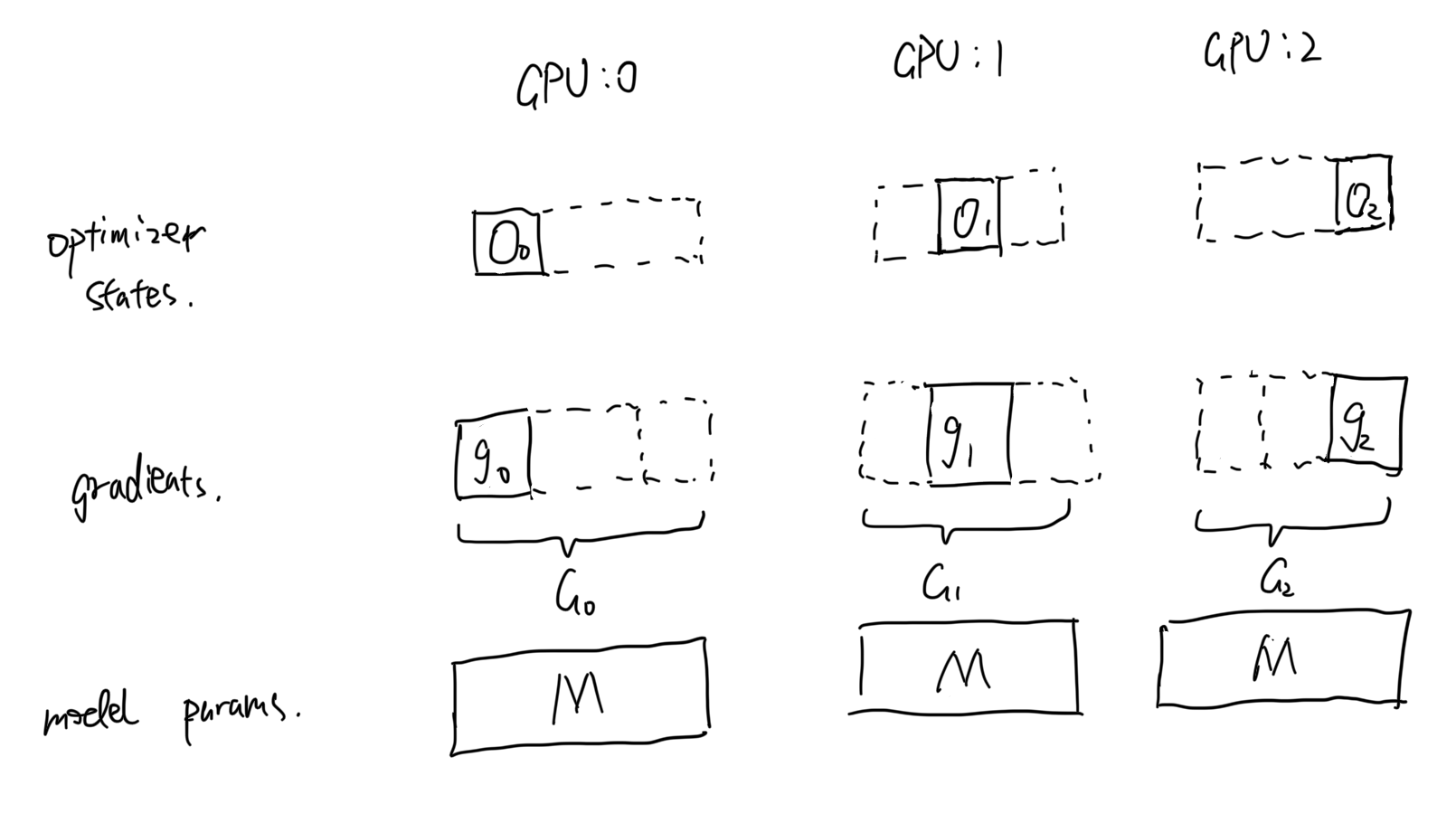 3. O + G + **Model Weights(M)**: So far we have optimized memory usage of tensors related to backward($O$ and $G$), how about tensors used for forward pass, the model parameter? In DP forward pass, each worker does forward computation independently with full model parameters, and it sounds tricky that how it can be optimized. Actually, the idea behind model weights optimization is "fetch and compute" and "dispose it after compute". Suppose we have three model layers and two GPUs. $W_{xy}$ denotes xth layer's yth partition. For example, $W_{10}$ means the second layer weight on the first GPU. Suppose we forward pass the second layer on first GPU, we need to all-gather $W_{10}$ on local gpu and $W_{11}$ on the second GPU to materialize the second layer $W_{1}$. Afterwards, it discards $W_{1}$ and repeat the layer materialization step described. Therefore, the peak memory usage on each GPU (for model parameter only) is only the one layer weight in this example. 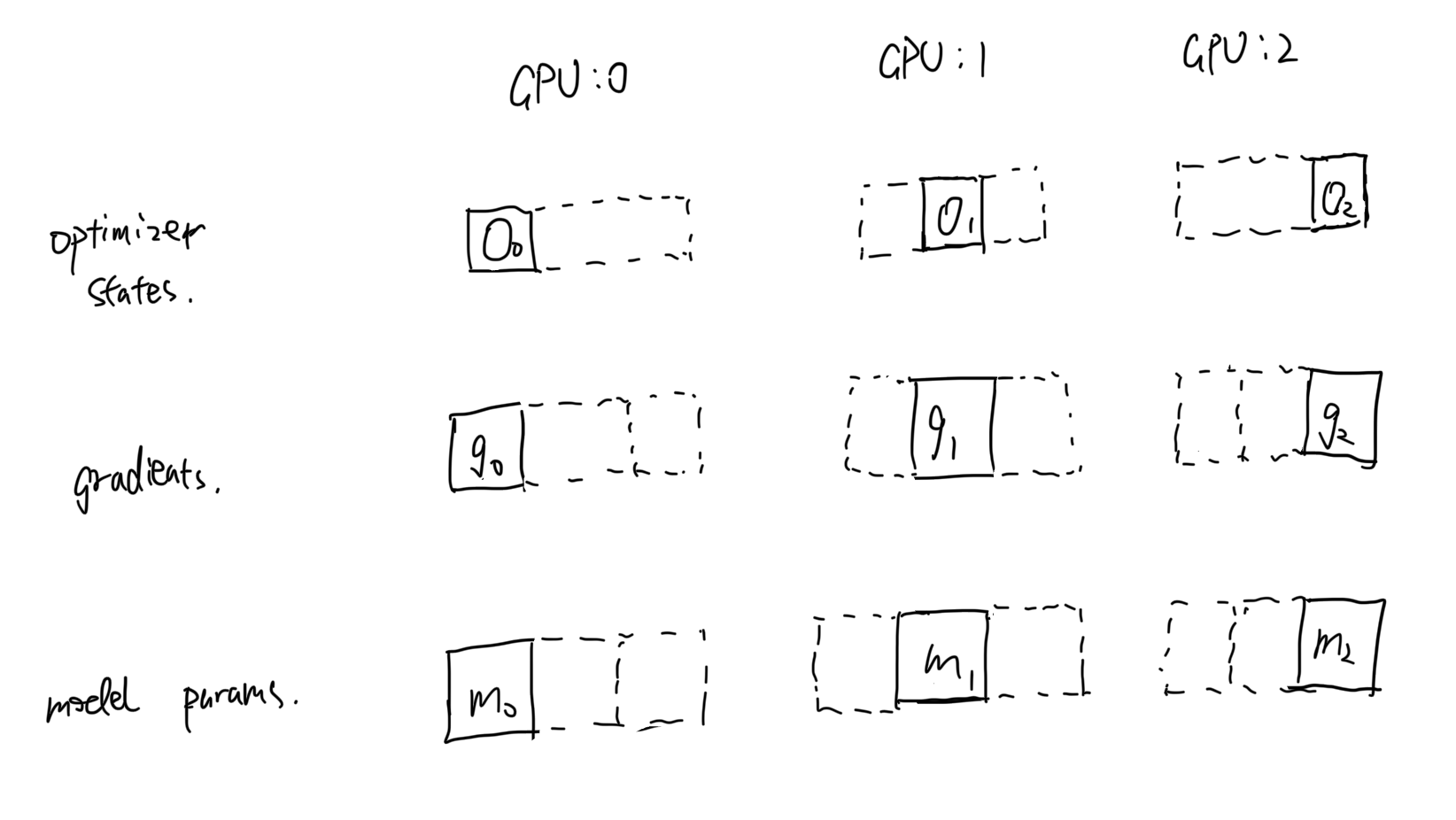 In practice, Zero-3 could be significantly slower than DDP as the model is very large. The root cause is that the **granularity of model weights sharding unit is still not small enough to fully utilize compute-communication overlapping**. ## Fully Sharded Data Parallel Here is a snippet from FSDP paper: > The FSDP algorithm is motivated by the ZeroRedundancyOptimizer [27, 28] technique from DeepSpeed but with a revised design and implementation that is aligned with the other components of PyTorch. FSDP breaks down a model instance into smaller units and then flattens and shards all of the parameters within each unit. The sharded parameters are communicated and recovered on-demand before computations, and then they are immediately discarded afterwards. This approach ensures that FSDP only needs to materialize parameters from one unit at a time, which significantly reduces peak memory consumption FSDP (Fully Sharded Data Parallel) builds on the principle of Zero's third stage but with further optimizations that enhance performance, making it suitable for training large language models (LLMs) more efficiently. It proposes FSDP unit which is the smallest unit in FSDP that is turned into `FlatParameter` before sharding and materialized upon computation. On the one hand, it's more integrated with PyTorch ecosystem. On the other hand, FSDP unit is smaller than its equivalent "partition unit" in Zero3 which makes model weight fetching more streamlined and efficient w.r.t computation. An intuitive graph compares DeepSpeed simplified communication and computation time is shown below. $T_i$ represents the computation/communication time needed for ith "fetch and compute" unit.  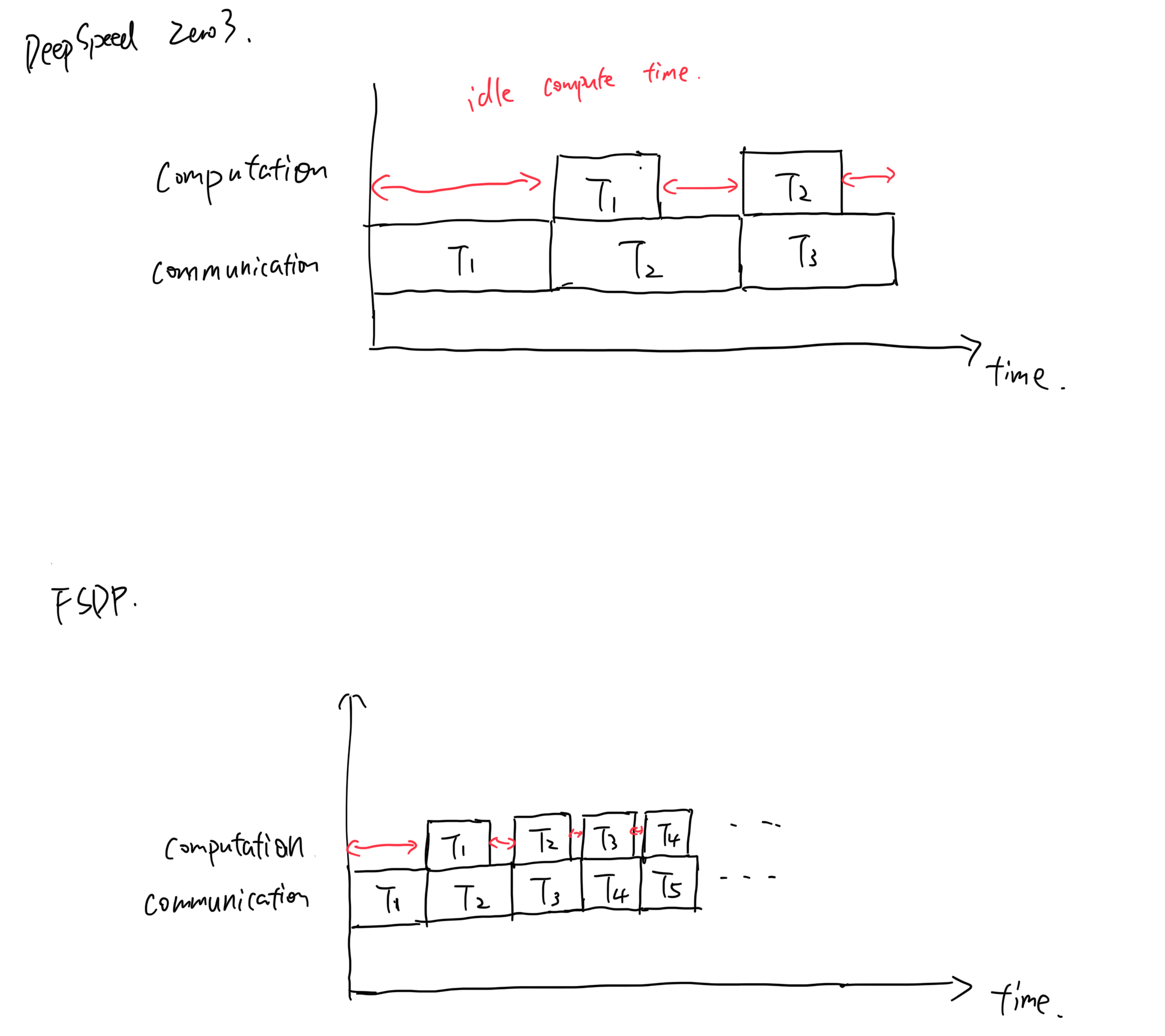I used the arrowed line in red to show the idle computation time difference between the two training frameworks. As the graph indicates, the smaller granularity of "fetch and compute" unit in FSDP enables less compute idle time. ## Q & A ### Q1: How does FSDP compare to Tensor Parallelism? There could be some common misunderstanding that FSDP is similar to Tensor Parallelism because they both partition model parameters and distribute across GPUs. However, they differ a lot if you really take a closer look at them. * **Fundamental difference**: FSDP is essentially data parallelism, and the model parameter sharding across GPUs is just a extra "feature" evolved to reduce model redundency. But TP by nature slices model weights and distributes across GPUs. * **Input weights and "splitting" methods difference**: Sharding is the process of flattening and partitioning, and it's model weight agnostic. In other words, it can shard any number of weights together into one FlatParameter and then partition based on the number of GPUs. However, TP needs to slice model weights along column dimension or row dimension depending on the matrix weight operation to make sure each GPU can compute logits more independently to reduce communication. In the MLP example above, we need to slice `w1` along row dimension and `w2` column dimension. * **GPU persistence difference**: During FSDP training, on each GPU, sharded weights are prefetched upon usage and disposed after usage. Therefore, FSDP doesn't persist full model weights on each GPU. However, for TP, model weights are partitioned, and they persist across GPUs during training. (Another view is that FSDP persists a shard of model parameter on each GPU.) ### Q2: How does FSDP compare to model parallelism? Similar to Q1, they differ from these three perspectives. The second point worth mentioning, MP partitions model weights inter-layer, and TP partitions model weights intra-layer. Intuitively, if you have input logits, FSDP partition on one GPU which doesn't form a full weight matrix is not enough for forward pass but one or more layers on one GPU from MP allows you do forward computation. ### Q3: Why there are $G_0$, $G_1$, and $G_2$ rather than a unified $G$? Gradients on each GPU is computed w.r.t their respective input data batch. In other words, each GPU takes different data batch and results in different gradients. They have the full shape as the model but values are different. Therefore, they need some `reduce` operations to average. ### Q4: Given that zero-2 has optimized communication than zero-1, do we always use zero-2 in pratice? In practice, when we are training very large models with hybrid parallelism in a multi-node setting, we often use zero-1 together with pipeline parallelism. The reason is that in zero-1, for a given PP stage, the gradient vector persists to accumulate for each microbatch and does `all-reduce` operation after all microbatches backwards completed and before optimization step. By contrast, the optimized communication in zero-2 requires gradient partitions but each PP micro-batch computation requires full gradients to accumulate gradients for each microbatch. Therefore, it requires `reduce-scatter` gradients for each microbatch for a given PP stage. Although theoretically we can still use zero-2(or even zero-3) and PP together, but the extra communication incurred for all microbatch doesn't worth it. The communication complexity for one stage are $O(3\theta)$ (Zero-1 + PP) and $O(\theta+M \theta)$ (Zero-2 + PP) where $\theta$ is the parameter size on the stage device and $M$ is the micro-batch size for PP.